2019/07/23
垂直線を扱えなかったので、X= **
の垂直線の値を扱えるようにしました。
双曲線と直線の交点
双曲線と直線の交点、更に弓型部、扇型部の面積、弓型部弧の長さの計算をします。
双曲線の弓型部、扇型部の面積では、双曲線 X2/a2
- Y2/b2
= 1 の双曲線でしたが、ここでは計算の都合上 X2/a2
- Y2/b2
= -1 の双曲線です。
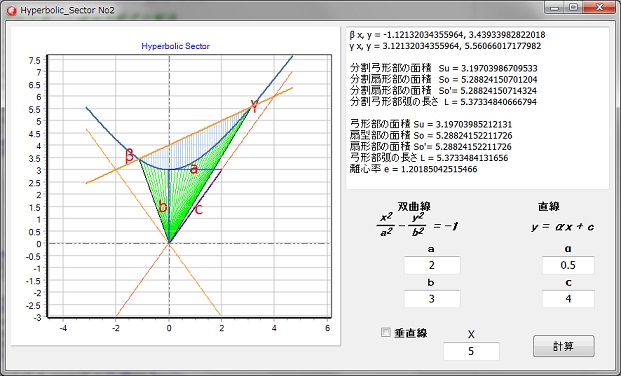双曲線の向きが、X軸方向からY軸方向に変わるだけで、基本的な計算は変わりません。
直線 y = αx + c の α の値がゼロ以外は、左右対称とならないので、左半分と、右半分に分けて計算します。
直線の傾きが漸近線の傾きと等しい場合は、交点が一か所となり、漸近線の傾きより大きい場合は上下の双曲線に交点が発生します。
直線の傾きが、漸近線の傾きより小さい場合は、交点が無いか、同じ方向の双曲線二か所の交点か、どちらかの双曲線の接線となります。
垂直の線を入力する場合は、垂直線にチェックを入れて、Xの値をしていします。
交点は、双曲線と直線の連立方程式を解けば容易に求める事ができます。
二次方程式なので、特に解説は必要無いでしょう。
面積と弧の長さの検算は、分割積分と比較して正しいかどうか確認しています。
計算式自体は、公式を使用していますが、プログラムミスの確認の為、分割積分を追加で行っています。
β点、原点、γ点での三角形の面積は、三点の座標による面積計算を行っています。
扇型部の面積が二つあるのは計算式を変えて計算した結果で、単に確認用です。
分割計算の場合は、値は完全には一致しません。
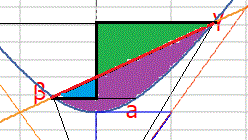この弓型部の面積を計算する方法は、直線と交点 β、γ と
交点からY軸に対する垂線で出来る三角形の面積で基本式の面積を補正して計算します。
交点
β、γ のX方向位置が同じ方向になってしまう場合は、小さい方の弓型部の面積の符号に注意が必要です。
この計算は、単に:計算結果が正しいかどうかの確認の為に計算方法を変えて行っています。
γ(-x,y) 原点 γ(x,y) と β(-x,y) 原点 β(x,y) の二等辺三角形の面積からそれぞれの扇形部の面積を差し引いて計算した面積をもとにして計算しています。
扇形部の面積は二つ計算し、その後βγ間の傾きで補正します。
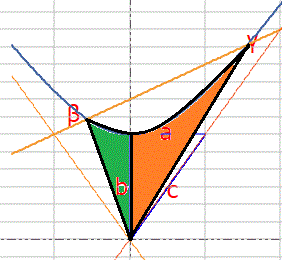
左図扇形部の面積は βy と γy の値で次の計算式でそれぞれ面積を計算し加算すれば簡単に求める事ができます。:
S1 = a * b * arccosh(βy / b) / 2
S2 = a * b * arccosh(γy
/ b) / 2
S = S1 + S2
弓形部の面積は、β 原点 γ 三点の座標の三角形の面積から扇形部の面積を差し引けば計算されます。
前記の弓形部の面積計算は、γ(-x,y) 原点 γ(x,y) と β(-x,y) 原点 β(x,y) の二等辺三角形の面積からそれぞれの扇形部の面積を差し引いて計算した面積をもとにして計算しています。
扇形部の面積は二つ計算し、その後βγ間の傾きで補正します。
双曲線と直線の図は、TChartの線グラフと、TChartのBackImageで表示しています。
TChartにもCanvasがあり、そこへ文字や図形を描画出来るのですが、最小化し、再度表示すると消えてしまいます、これは、TFormのCanvasに直接描画すると、最小化したり、裏表示になつたりすると消えてしまう現象と同じです。
原因は、Bitmap がなく、一旦消えてしまうと再生出来ない為です。
そこで、TChartと同じサイズのTImageを用意して、TImageのBitmapに書き込んだ後、TChartのBackImageのBitmapにコピーして、表示しています。
TImageは非表示にしておきます。
TChartを使用せず、全てをTImageに書き込んで゛も良いのですが、TChartを使用した方が、グラフの作成が簡単です。
TChartを使用する場合の注意点は、AutoSizeにしておいて、グラフデーター配列に追加する場合、追加が終了した時点で、グラフ表示の為の割り込み処理を実行させないと、グラフの情報を正しく読みだすことが出来ません。
データーの追加が終わった時点で、Application.ProcessMessagesを実行して、追加データーの表示をさせれば、データー追加後のグラフ情報を正しく得ることが出来ます。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series,
Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart, Vcl.StdCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Chart1: TChart;
Series1: TLineSeries;
Series2: TLineSeries;
Series3: TLineSeries;
Series4: TLineSeries;
Series5: TLineSeries;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
Memo1: TMemo;
Series6: TLineSeries;
LabeledEdit4: TLabeledEdit;
Series7: TLineSeries;
Image1: TImage;
Image2: TImage;
CheckBox1: TCheckBox;
LabeledEdit5: TLabeledEdit;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
private
{ Private 宣言 }
function fy: boolean;
procedure Linedraw;
procedure Textdraw;
procedure area(bx, by, gx, gy: double);
procedure second_imperfect_elliptic_integral(z, K: double; var F, E: Double);
procedure arch(bx, gx, by, gy: double);
procedure integral(betax, gammaX: double);
procedure archpaint(bx, by, gx, gy: double);
procedure Image2Draw;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses math;
var
a, b : double; // 双曲線系数
alpha, d : double; // 直線係数
xinp : double; // 垂線の位置
xpL, xpR : integer;
xpF : boolean;
procedure TForm1.Button1Click(Sender: TObject);
label
ENDNP;
var
ch : integer;
chF : boolean;
begin
button1.Enabled := False;
chF := True;
val(LabeledEdit1.Text, a, ch);
if ch <> 0 then begin
application.MessageBox('ａの値に間違いがあります。','注意',0);
chF := False;
goto ENDNP;
end;
if a = 0 then begin
application.MessageBox('ａがゼロです。','注意',0);
chF := False;
goto ENDNP;
end;
val(LabeledEdit2.Text, b, ch);
if ch <> 0 then begin
application.MessageBox('ｂの値に間違いがあります。','注意',0);
chF := False;
goto ENDNP;
end;
if b = 0 then begin
application.MessageBox('bがゼロです。','注意',0);
chF := False;
goto ENDNP;
end;
if not checkBox1.Checked then begin
val(LabeledEdit3.Text, alpha, ch);
if ch <> 0 then begin
application.MessageBox('αの値に間違いがあります。','注意',0);
chF := False;
goto ENDNP;
end;
val(LabeledEdit4.Text, d, ch);
if ch <> 0 then begin
application.MessageBox('dの値に間違いがあります。','注意',0);
chF := False;
end;
end
else begin
val(LabeledEdit5.Text, Xinp, ch);
if ch <> 0 then begin
application.MessageBox('dの値に間違いがあります。','注意',0);
chF := False;
end;
end;
ENDNP:
if not chF then begin
button1.Enabled := True;
exit;
end;
a := abs(a);
b := abs(b);
fy;
button1.Enabled := True;
end;
// 弓形部,扇形部の面積、長さの分割積分確認計算
procedure TForm1.integral(betax, gammaX: double);
var
i, n : integer;
dx, dx2 : double;
b2, b2sa2 : double;
s, x : double;
x0, x1 : double;
y0, y1 : double;
L, dl : double;
ds, ss : double;
sl, sr, aa : double;
begin
memo1.Lines.Add('');
s := 0;
n := 10000; // 分割数
dx := (gammaX - betaX) / n; // Δx
dx2 := dx / 2; // 中間点 Δx/2
b2 := b * b;
b2sa2 := b * b / a / a;
for i:= 0 to n - 1 do begin // 積分計算
x := i * dx + dx2 + betaX;
y0 := alpha * x + d; // 直線のy値
y1 := sqrt(b2 + b2sa2 * x * x); // 双曲線のy値
s := s + abs(abs(y0) - y1);
end;
s := s * dx;
memo1.Lines.Add('分割弓形部の面積 Su = ' + floatTostr(s));
L := 0; // 弧の長さ
x0 := betaX; // 最初のx計算
y0 := sqrt(b2 + b2sa2 * x0 * x0); // 最初のy計算
for i := 1 to n do begin // 積分計算
x1 := i * dx + betaX; // 双曲線x
y1 := sqrt(b2 + b2sa2 * x1 * x1); // 双曲線y
dl := sqrt((x1 - x0) * (x1 - x0) + (y1 - y0) * (y1 - y0)); // 微小長さΔL
L := L + dl; // 合計値
x0 := x1;
y0 := y1;
end;
y0 := sqrt(b2 + b2sa2 * betaX * betaX); // 双曲線のbetaXの位置のyの値
y1 := sqrt(b2 + b2sa2 * gammaX * gammaX); // 双曲線のgammaXの位置のyの値
dx := (abs(gammaX) + abs(betaX)) / n; // Δx
dx2 := dx / 2; // 中間点 Δx/2
sl := 0; // 扇形部左
if abs(betaX) > dx then begin
aa := abs(y0 / betaX); // 直線左の傾き
for i := 0 to round(abs(betaX / dx)) - 1 do begin
x := i * dx + dx2;
ds := (sqrt(b2 + b2sa2 * x * x) - aa * x) * dx; // Δs
sl := sl + ds;
end;
end;
sr := 0; // 扇形部左
if abs(gammaX) > dx then begin
aa := abs(y1 / gammaX); // 直線右の傾き
for i := 0 to round(abs(gammaX / dx)) - 1 do begin
x := i * dx + dx2;
ds := (sqrt(b2 + b2sa2 * x * x) - aa * x) * dx; // Δs
sr := sr + ds;
end;
end;
if gammaX * betaX <= 0 then aa := sl + sr
else aa := abs(sl - sr);
ds := abs(betaX * y1 - gammaX * y0) / 2; // 三角形面積
ss := ds - s; // 扇形部面積
memo1.Lines.Add('分割扇形部の面積 So = ' + floatTostr(aa));
memo1.Lines.Add('分割扇形部の面積 So''= ' + floatTostr(ss));
memo1.Lines.Add('分割弓形部弧の長さ L = ' + floatTostr(L));
end;
//-------------------------------
// 第１種第２種楕円積分
// FBnKn[0] 第１種楕円積分解
// EBnKn[0] 第２種楕円積分解
// ランデン変換
// Q 角度 deg
// K 離心率
//-------------------------------
procedure TForm1.second_imperfect_elliptic_integral(z, K: double; var F, E: Double);
var
I, MI : integer;
Kn : array of double; // Kn
knd : array of double; // k'n
N2SKn : array of double; // 2/(1+Kn)
T2SKnd : array of double; // П2/(1+Kn')
BRad : array of double; // β(rad)
SinBn : array of double; // sinβn
FBnKn : array of double; // F(βn,kn)
EBnKn : array of double; // E(βn,kn)
LnD : double;
Q : double;
begin
// K = 0 の時は円なのでpiの角度値radをかえします。
Q := arcsin(z);
if K = 0 then begin
E := Q;
F := E;
exit;
end;
// この時は１をかえします 演算エラー防止の為、値は正しくありません。
if (K = 1) and (Q >= pi / 2) then begin
E := 1;
F := 1;
exit;
end;
// (1 > K > 0 and Q <= 90°) or (K = 1 and Q < 90°)の時
MI := 0;
LND := 0;
setlength(kn, MI + 1); // kn
kn[0] := K;
while LND <> Kn[MI] do begin
LnD := Kn[MI];
inc(MI);
setlength(kn, MI + 1); // kn
kn[MI] := 2 * sqrt(Kn[MI - 1])/(1 + Kn[MI - 1]);
end;
Dec(MI);
setlength(kn, MI + 1); // kn
setlength(knd, MI + 1); // k'n
setlength(N2SKn, MI + 1); // 2/(1+Kn)
setlength(T2SKnd, MI + 1); // П2/(1+Kn')
setlength(BRad, MI + 1); // β(rad)
setlength(SinBn, MI + 1); // sinβn
setlength(FBnKn, MI + 1); // F(βn,kn)
setlength(EBnKn, MI + 1); // E(βn,kn)
knd[0] := 1;
for I := 1 to MI do
knd[I] := (1 - kn[I - 1]) / (1 + Kn[I - 1]);
for I := 0 to MI do
N2SKn[I] := 2 / (1 + kn[I]);
T2SKnd[MI] := N2SKn[MI];
for I := MI - 1 downto 0 do
T2SKnd[I] := T2SKnd[I + 1] * N2SKn[I];
BRad[0] := Q;
for I := 1 to MI do
BRad[I] := (arcsin(kn[I - 1] * sin(Brad[I - 1])) + Brad[I - 1]) / 2;
for I := 0 to MI do
SinBn[I] := sin(Brad[I]);
LnD := LN((1 + sin(Brad[MI])) / cos(Brad[MI]));
for I := 0 to MI do
FBnKn[I] := T2SKnd[I] * LnD;
F := FBnKn[0];
EBnKn[MI] := sin(Brad[MI]);
for I := MI - 1 downto 0 do
EBnKn[I] := (2 * EBnKn[I + 1] + 2 * knd[I + 1] * FBnKn[I + 1]) / (1 + knd[I + 1]) - kn[I] * SinBn[I];
E := EBnKn[0];
end;
// 双曲弧の長さ計算
procedure TForm1.arch(bx, gx, by, gy: double);
var
e, k, z : double;
Fzk, Ezk : double;
L, Ll, Lr, x : double;
begin
e := sqrt(b * b + a * a) / b; // 離心率e
k := 1 / e; // k
x := abs(by);
z := sqrt((x * x - b * b) / (x * x - k * k * b * b)); // z
second_imperfect_elliptic_integral(z, k, Fzk, Ezk); // 第一種第二種楕円積分
Ll := (b * (1 - k * k) * Fzk - b * Ezk + x * z) / k; // Ll
if bx > 0 then Ll := -Ll; // 交点βがγと同じ側の場合
x := abs(gy);
z := sqrt((x * x - b * b) / (x * x - k * k * b * b)); // z
second_imperfect_elliptic_integral(z, k, Fzk, Ezk); // 第一種第二種楕円積分
Lr := (b * (1 - k * k) * Fzk - b * Ezk + x * z) / k; // Ll
if gx < 0 then Lr := -Lr; // 交点γがβと同じ側の場合
L := Ll + Lr;
memo1.Lines.Add('弓形部弧の長さ L = ' + floatTostr(L));
memo1.Lines.Add('離心率 e = ' + floatTostr(e));
end;
// 双曲線 弓形部と扇形部の面積
procedure TForm1.area(bx, by, gx, gy: double);
var
x4, s4 : double;
v4 : double;
s1, sl, sr : double;
b2, b2sa2 : double;
y0, y1 : double;
ds, ss, s : double;
begin
memo1.Lines.Add('');
by := abs(by);
gy := abs(gy);
// 左側の計算 二倍の値が計算されます
sbl := a * b * arccosh(by / b); // 扇型面積
x4 := a / b * sqrt(by * by - b * b); // x = by , y = x4
s4 := by * x4 - sbl; // 弓形面積 = 三角面積 - 扇形面積
if bx > 0 then begin // 交点βがγと同じ側の場合
s4 := -s4;
sbl := -sbl;
end;
v4 := (gy - by) * bx / (gx - bx); // 補正三角部高さ
s1 := bx * v4; // 補正三角部面積
sl := (s4 + s1); // 左側の値
// 右側の計算 二倍の値が計算されます
sbr := a * b * arccosh(gy / b); // 扇型面積
x4 := a / b * sqrt(gy * gy - b * b); // x = gy , y = x4
s4 := gy * x4 - sbr; // 弓形面積 = 三角面積 - 扇形面積
if gx < 0 then begin // 交点γがβと同じ側の場合
s4 := -s4;
sbr := -sbr;
end;
v4 := (gy - by) * gx / (gx - bx); // 補正三角部高さ
s1 := gx * v4; // 補正三角部面積
sr := (s4 - s1); // 右側の値
sb := (sbl + sbr) / 2; // 左右加算の二分の一
s := (sl + sr) / 2; // 左右加算の二分の一
memo1.Lines.Add('弓形部の面積 Su = ' + floatTostr(s));
memo1.Lines.Add('扇型部の面積 So = ' + floatTostr(sb));
// 三点の値 bx,y, 0,0 gx,gy の面積 - 弓形面積
b2 := b * b;
b2sa2 := b * b / a / a;
y0 := sqrt(b2 + b2sa2 * bx * bx); // 双曲線のbxの位置のyの値
y1 := sqrt(b2 + b2sa2 * gx * gx); // 双曲線のgxの位置のyの値
ds := abs(bx * y1 - gx * y0) / 2; // 三角形面積
ss := ds - s; // 扇形部面積
memo1.Lines.Add('扇形部の面積 So'= ' + floatTostr(ss));
end;
// 扇型部塗りつぶし
procedure TForm1.archpaint(bx, by, gx, gy: double);
var
i, n : integer;
dx : double;
dpx, dpy : double;
xmin, ymin : double;
xmax, ymax : double;
px0, py0 : integer;
pxmin, pymin : integer;
pxmax, pymax : integer;
xp1, yp1 : integer;
xp2, yp2 : integer;
xf1, yf1 : double;
b2, b2sa2 : double;
xf2 : double;
begin
ymin := Chart1.LeftAxis.Minimum;
ymax := Chart1.LeftAxis.Maximum;
xmin := Chart1.BottomAxis.Minimum;
xmax := Chart1.BottomAxis.Maximum;
if d > 0 then begin
px0 := Series7.CalcXPos(0);
py0 := Series7.CalcYPos(0);
end
else begin
px0 := Series7.CalcXPos(2);
py0 := Series7.CalcYPos(2);
end;
pxmin := Series4.CalcXPos(1);
pymin := Series4.CalcYPos(1);
pxmax := Series4.CalcXPos(2);
pymax := Series4.CalcYPos(0);
dpy := (pymax - pymin) / (ymax - ymin); // pymax < pymin に注意
dpx := (pxmax - pxmin) / (xmax - xmin);
b2 := b * b;
b2sa2 := b * b / a / a;
xf1 := dpx * bx;
xf2 := dpx * gx;
dx := (gx - bx) / (xf2 - xf1) * 5;
n := round(abs(xf2 - xf1) / 5);
Image1.Canvas.Pen.Color := clLime;
Image1.Canvas.Pen.Style := psSolid;
Image1.Canvas.Pen.Width := 1;
for i:= 0 to n - 1 do begin
xf1 := i * dx + bx;
yf1 := sqrt(b2 + b2sa2 * xf1 * xf1); // 双曲線のy値
xp1 := round(dpx * (xf1)) + px0;
xp2 := px0;
if d > 0 then begin // 双曲線+-側で計算変更
yp1 := py0 + round(dpy * yf1);
yp2 := py0;
end
else begin
yp1 := py0 + round(dpy * -yf1);
yp2 := py0;
end;
Image1.Canvas.MoveTo(xp1, yp1);
Image1.Canvas.LineTo(xp2, yp2);
end;
end;
// TImageに文字出力
procedure TForm1.Textdraw;
var
xpp, ypp: integer;
begin
Image1.Canvas.Font.Size := 17; // 文字の高さ
Image1.Canvas.Font.Color := clRed;
Image1.Canvas.Font.Name := 'Tahoma';
xpp := (Series7.CalcXPos(0) + Series7.CalcXPos(2)) div 2 - 7; // 文字aのx位置計算
ypp := Series7.CalcyPos(1) - 17; // 文字aのy位置計算
Image1.Canvas.TextOut(xpp, ypp, 'a'); // aの描画
xpp := Series7.CalcXPos(1) - 15; // 文字bのx位置計算
ypp := Series7.CalcYPos(0) - ((Series7.CalcYPos(0) - Series7.CalcYPos(2)) div 2) - 15; // 文字bのy位置計算
Image1.Canvas.TextOut(xpp, ypp, 'b'); // bの描画
xpp := (Series7.CalcXPos(0) + Series7.CalcXPos(2)) div 2 - 12; // 文字cのx位置計算
ypp := Series7.CalcYPos(0) - (Series7.CalcYPos(0) - Series7.CalcYPos(2)) div 2;
if d > 0 then begin
xpp := xpp + 12;
ypp := ypp - 12; // 文字cのy位置計算
end
else begin
xpp := xpp - 12;
ypp := ypp - 12; // 文字cのy位置計算
end;
Image1.Canvas.TextOut(xpp, ypp, 'c'); // cの描画
if d > 0 then begin
xpp := Series1.CalcXPos(xpL) - 20;
ypp := Series1.CalcYPos(xpL) - 20;
Image1.Canvas.TextOut(xpp, ypp, 'β'); // βの描画
end
else begin
xpp := Series3.CalcXPos(xpL) - 20;
ypp := Series3.CalcYPos(xpL) - 20;
Image1.Canvas.TextOut(xpp, ypp, 'β'); // βの描画
end;
if d > 0 then begin
xpp := Series1.CalcXPos(xpR);
ypp := Series1.CalcYPos(xpR) - 20;
Image1.Canvas.TextOut(xpp, ypp, 'γ'); // βの描画
end
else begin
xpp := Series3.CalcXPos(xpR);
ypp := Series3.CalcYPos(xpR) - 20;
Image1.Canvas.TextOut(xpp, ypp, 'γ'); // βの描画
end;
end;
// 直線の描画
procedure TForm1.Linedraw;
var
i : integer;
xp1, yp1: integer;
xp2, yp2: integer;
begin
xp1 := Series7.CalcXPos(0); // 双曲線原点X
yp1 := Series7.CalcYPos(0); // 双曲線原点y
xp2 := Series7.CalcXPos(2); // グラフ原点 x0
yp2 := Series7.CalcYPos(2); // グラフ原点 y0
Image1.Canvas.Pen.Color := clBlue;
Image1.Canvas.Pen.Width := 2;
Image1.Canvas.Pen.Style := psSolid;
Image1.Canvas.MoveTo(xp1,yp1); // c の線
Image1.Canvas.LineTo(xp2,yp2);
application.ProcessMessages;
Image1.Canvas.Pen.Color := clskyblue;
Image1.Canvas.Pen.Width := 1;
Image1.Canvas.Pen.Style := psSolid;
for i := xpL to xpR do begin // 双曲線弓形部塗りつぶし
if i mod 2 = 0 then begin
if d < 0 then begin
xp1 := Series3.CalcXPos(i); // 双曲線-y側座標
yp1 := Series3.CalcYPos(i);
end;
if d > 0 then begin
xp1 := Series1.CalcXPos(i); // 双曲線+y側座標
yp1 := Series1.CalcYPos(i);
end;
xp2 := Series2.CalcXPos(i); // 直線座標
yp2 := Series2.CalcYPos(i);
Image1.Canvas.MoveTo(xp1,yp1);
Image1.Canvas.LineTo(xp2,yp2);
end;
end;
Image1.Canvas.Pen.Color := clblack;
Image1.Canvas.Pen.Width := 1;
Image1.Canvas.Pen.Style := psDashdotdot;
xp1 := Series4.CalcXPos(0);
xp2 := Series4.CalcXPos(2);
if d > 0 then
yp1 := Series7.CalcYPos(0) // y = 0 の座標
else
yp1 := Series7.CalcYPos(2); // y = 0 の座標
yp2 := yp1;
Image1.Canvas.MoveTo(xp1,yp1); // X軸線
Image1.Canvas.LineTo(xp2,yp2);
if d > 0 then
xp1 := Series7.CalcXPos(0) // x = 0 の座標
else
xp1 := Series7.CalcXPos(2); // x = 0 の座標
xp2 := xp1;
yp1 := Series4.CalcYPos(0);
yp2 := Series4.CalcYPos(1);
Image1.Canvas.MoveTo(xp1,yp1); // y軸線
Image1.Canvas.LineTo(xp2,yp2);
if d > 0 then begin
xp1 := Series1.CalcXPos(xpl); // beta x
yp1 := Series1.CalcYPos(xpl); // beta y
end
else begin
xp1 := Series3.CalcXPos(xpl); // beta x
yp1 := Series3.CalcYPos(xpl); // beta y
end;
if d > 0 then begin
xp2 := Series7.CalcXPos(0); // x 0
yp2 := Series7.CalcYPos(0); // y 0
end
else begin
xp2 := Series7.CalcXPos(2); // x 0
yp2 := Series7.CalcYPos(2); // y 0
end;
Image1.Canvas.Pen.Style := psSolid;
Image1.Canvas.MoveTo(xp1,yp1); // beta x,y -> 0,0
Image1.Canvas.LineTo(xp2,yp2);
if d > 0 then begin
xp1 := Series1.CalcXPos(xpR); // gamma x
yp1 := Series1.CalcyPos(xpR); // gamma y
end
else begin
xp1 := Series3.CalcXPos(xpR); // gamma x
yp1 := Series3.CalcyPos(xpR); // gamma y
end;
Image1.Canvas.LineTo(xp1,yp1); // 0,0 -> gamma x,y の線
end;
// 双曲線の描画
function TForm1.fy: boolean;
label
XPOS;
const
nk100 = 100; // 双曲線分割数
var
betaX, betaY : double; // 双曲線と直線の交点β
gammaX, gammaY : double; // 双曲線と直線の交点γ
a0, b0, c0 : double; // a0x^2 + b0x + c0 = 0
e0, f0 : double;
i, n, k : integer;
dx, y, x : double;
Xmax, Xmin, Ymax, Ymin : double;
asb : double; // 漸近線傾斜係数
sbF : integer; // 漸近線フラグ
bx, gx : double;
begin
result := false;
xpF := false;
Image1.Canvas.Brush.Style := bsSolid;
Image1.Canvas.FillRect(rect(0,0,Image1.Width,Image1.Height));
Image1.Canvas.Brush.Style := bsClear;
chart1.BackImage.Bitmap := Image1.Picture.Bitmap;
memo1.Clear;
Series1.Clear; // 双曲線+側
Series2.Clear; // y = a/b * x
Series3.Clear; // 双曲線-側
Series4.Clear; // スケール設定
Series5.Clear; // 漸近線
Series6.Clear; // 漸近線
Series7.Clear; // abc 三角
sbF := 0; // 漸近線フラグ
betaX := 0;
gammaX := 0;
betaY := 0;
gammaY := 0;
bx := 0;
gx := 0;
a0 := 0;
e0 := 0;
if checkbox1.Checked then goto XPOS;
// 交点計算 連立方程式の解法
a0 := 1 / a / a - alpha * alpha / b / b;
b0 := - 2 * alpha * d / b / b;
c0 := - d * d / b / b + 1;
e0 := b0 * b0 - 4 * a0 * c0;
if e0 < 0 then begin
memo1.Lines.Add('交点無し');
betaX := -(a + b) / 2 * 5;
gammaX := (a + b) / 2 * 5;
sbF := 1;
end
else begin // 同じ双曲線に交点二か所あり
if a0 <> 0 then begin
xpF := true;
f0 := sqrt(e0);
betaX := (- b0 - f0) / 2 / a0;
betaY := alpha * betax + d;
gammaX := (- b0 + f0) / 2 / a0;
gammaY := alpha * gammax + d;
memo1.Lines.Add('β x, y = ' + floatTostr(betax) + ', ' + floatTostr(betay));
memo1.Lines.Add('γ x, y = ' + floatTostr(gammax) + ', ' + floatTostr(gammay));
end;
end;
application.ProcessMessages; // memo1出力を確定させます
if e0 = 0 then begin
if d <> 0 then memo1.Lines.Add('接線');
betaX := -(a + b);
gammaX := (a + b);
sbf := 2;
end;
if betaY * gammaY < 0 then begin
memo1.Lines.Add('上下双曲線に対する直線');
x := abs(betaX);
y := abs(gammaX);
if x > y then begin
betaX := -x;
gammaX := x;
end
else begin
betaX := -y;
gammaX := y;
end;
sbF := 3;
end;
if a0 = 0 then begin
if b0 <> 0 then begin
memo1.Lines.Add('交点一か所 漸近線と平行');
betaX := c0 / b0;
betaY := alpha * betax + d;
memo1.Lines.Add('β x, y = ' + floatTostr(betax) + ', ' + floatTostr(betay));
betaX := -(a + b);
gammaX := (a + b);
end
else begin
memo1.Lines.Add('交点無し 漸近線と平行');
end;
sbF := 4;
end;
XPOS:
if checkbox1.Checked then begin
bx := xinp;
gx := xinp;
betax := xinp;
gammax := xinp;
if xinp < 5 then begin
betax := 5;
gammax := 5;
end;
dx := 1 + xinp * xinp / a / a;
y := sqrt(dx * b * b);
betay := y;
gammay := -y;
sbF := 5;
memo1.Lines.Add('上下双曲線に対する直線');
memo1.Lines.Add('β x, y = ' + floatTostr(bx) + ', ' + floatTostr(betay));
memo1.Lines.Add('γ x, y = ' + floatTostr(gx) + ', ' + floatTostr(gammay));
end;
application.ProcessMessages; // memo1出力を確定させます
dx := abs((gammaX - betaX) / nk100);
xmax := gammaX * 1.5;
xmin := betaX * 1.5;
if abs(betaX) > abs(gammaX) then begin
xmax := abs(betaX);
xmin := - abs(betaX) * 1.5;
end;
if abs(betaX) < abs(gammaX) then begin
xmax := abs(gammaX) * 1.5;
xmin := - abs(gammaX);
end;
if abs(betaX) = abs(gammaX) then begin
xmax := abs(gammaX) * 1.5;
xmin := - abs(betaX) * 1.5;
end;
xpl := 0;
xpR := 0;
if dx <> 0 then n := round((xmax - xmin) / dx)
else begin
n := nk100;
dx := (xmax - xmin) / n
end;
asb := b / a;
for i := 0 to n do begin
x := i * dx + xmin;
if x < betaX then xpL := i;
if x < gammaX then xpR := i;
y := sqrt((1+ x * x / a / a) * b * b); // 双曲線y計算
if a0 <> 0 then begin
if (betay > 0) and (gammay > 0) then Series1.AddXY(x, y); // +双曲線
if (betay < 0) and (gammay < 0) then Series3.AddXY(x, -y); // -双曲線
if (betay * gammay < 0) then begin
Series1.AddXY(x, y); // +双曲線
Series3.AddXY(x, -y); // -双曲線
end;
end;
if (a0 = 0) or (e0 < 0) then begin
Series1.AddXY(x, y); // +双曲線
Series3.AddXY(x, -y); // -双曲線
end;
y := asb * x;
if sbF = 0 then begin
if d > 0 then begin
if x > -a then Series5.AddXY(x, y); // +漸近線
end
else if x < a then Series5.AddXY(x, y);
end
else Series5.AddXY(x, y);
y := -asb * x;
if sbF = 0 then begin
if d > 0 then begin
if x < a then Series6.AddXY(x, y); // -漸近線
end
else if x > -a then Series6.AddXY(x, y);
end
else Series6.AddXY(x, y);
end;
Chart1.Update;
application.ProcessMessages; // グラフ出力を確定させます
ymin := Chart1.LeftAxis.Minimum;
ymax := Chart1.LeftAxis.Maximum;
k := 0;
if not checkbox1.Checked then begin
for i := 0 to n do begin
x := i * dx + xmin;
y := alpha * x + d; // 直線y計算
if (y <= ymax * 1.5) and (y >= ymin * 1.5) then begin
Series2.AddXY(x, y); // 直線
inc(k);
end;
end;
end;
if k < 3 then begin
Series2.Clear;
Series2.AddXY(bx, ymin * 1.5); // 直線
Series2.AddXY(gx, ymax * 1.5); // 直線
end;
Chart1.Update;
application.ProcessMessages; // グラフ出力を確定させます
xmin := Chart1.BottomAxis.Minimum;
xmax := Chart1.BottomAxis.Maximum;
ymin := Chart1.LeftAxis.Minimum;
ymax := Chart1.LeftAxis.Maximum;
if (xmax - xmin) > (ymax - ymin) then begin
dx := ((xmax - xmin) - (ymax - ymin)) / 2;
ymin := ymin - dx;
ymax := ymax + dx;
end
else begin
dx := ((ymax - ymin) - (xmax - xmin)) / 2;
xmin := xmin - dx;
xmax := xmax + dx;
end;
Series4.AddXY(xmin, ymax); // スケール設定
Series4.AddXY(xmin, ymin);
Series4.AddXY(xmax, ymin);
Chart1.Update;
application.ProcessMessages; // グラフ出力を確定させます
if sbF <> 0 then exit;
if d > 0 then begin
Series7.AddXY(0, 0); // 一番小さい値から
Series7.AddXY(0, b); // bの線
Series7.AddXY(a, b); // aの線
end
else begin
Series7.AddXY(-a, -b); // 一番小さい値から
Series7.AddXY(0, -b); // aの線
Series7.AddXY(0, 0); // bの線
end;
application.ProcessMessages; // グラフ出力を確定させます
archpaint(betaX, betaY, gammaX, gammaY);
Linedraw;
Textdraw;
integral(betaX, gammaX);
area(betaX, betaY, gammaX, gammaY);
arch(betaX, gammaX, betaY, gammaY);
chart1.BackImage.Bitmap := Image1.Picture.Bitmap;
end;
// 双曲線直線式作図
procedure TForm1.Image2Draw;
begin
Image2.Canvas.Brush.Color := clBtnFace;
Image2.Canvas.Brush.Style := bsSolid;
Image2.Canvas.FillRect(rect(0, 0, Image2.Width, Image2.Height));
Image2.Canvas.Font.Name := 'MS UI Gothic';
Image2.Canvas.Font.Style := [fsItalic, fsBold];
Image2.Canvas.Font.Size := 12;
Image2.Canvas.Pen.Color := clBlack;
Image2.Canvas.Pen.Width := 2;
Image2.Canvas.Brush.Style := bsClear;
Image2.Canvas.Pen.Style := psSolid;
Image2.Canvas.MoveTo(20, 37);
Image2.Canvas.LineTo(45, 37);
Image2.Canvas.TextOut(25, 16, 'x');
Image2.Canvas.TextOut(25, 38, 'a');
Image2.Canvas.MoveTo(20 + 45, 37);
Image2.Canvas.LineTo(45 + 45, 37);
Image2.Canvas.TextOut(25 + 45, 16, 'y');
Image2.Canvas.TextOut(25 + 45, 38, 'b');
Image2.Canvas.Font.Size := 10;
Image2.Canvas.TextOut(34, 16, '2');
Image2.Canvas.TextOut(34, 38, '2');
Image2.Canvas.TextOut(34 + 45, 16, '2');
Image2.Canvas.TextOut(34 + 45, 38, '2');
Image2.Canvas.Font.Size := 13;
Image2.Canvas.TextOut(50, 29, '-');
Image2.Canvas.TextOut(100, 29, '= -1');
Image2.Canvas.TextOut(240, 29, 'y = αx + c');
Image2.Canvas.Font.Size := 11;
Image2.Canvas.Font.Style := [fsBold];
Image2.Canvas.TextOut(50, 2, '双曲線');
Image2.Canvas.TextOut(250, 2, '直線');
end;
procedure TForm1.FormCreate(Sender: TObject);
var
bm : Tbitmap;
begin
bm := Tbitmap.Create;
bm.Width := Chart1.Width;
bm.Height := Chart1.Height;
Image1.Width := Chart1.Width;
Image1.Height := Chart1.Height;
Image1.Visible := False;
Image1.Picture.Bitmap := bm;
Image1.Canvas.Brush.Color := clWhite;
bm.Width := Image2.Width;
bm.height := Image2.Height;
Image2.Picture.Bitmap := bm;
bm.Free;
Image2Draw;
end;
end.
Hyperbolic_SectorNo2.zip
各種プログラム計算例に戻る
最初に戻る