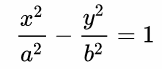
2019/09/30
メモリーリークがあったので修正しました。
2019/07/04
フォームを最小化して、元へ戻すと、グラフ部を残して、画像部が消えてしまうのを修正しました。
双曲線の弓形部の面積と弧長計算
双曲線の弓形部、扇形部、の面積と弧長の計算を行います。
双曲線の方程式
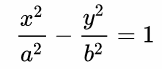
面積、弧長の計算式
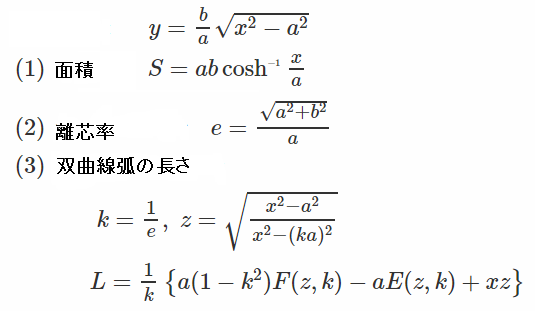
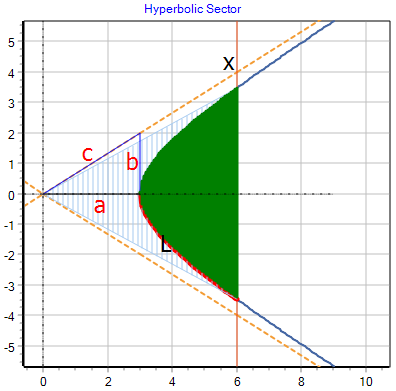
 左図は a=3,
b=2, x = 6 の時の計算結果です。
左図は a=3,
b=2, x = 6 の時の計算結果です。
弧の長さは、上図 赤線の部分です、全長ではないので注意してください。
弧の長さ計算には、第一、二種楕円積分を使用しています。
双曲線の弧の長さが、片側だけとなっているのは楕円積分の範囲に合わせている為のようです。
計算結果の確認には、微小範囲分割積分を使用して行っています、分割積分でも小数点以下三桁以上の精度を得ることが出来ます。
分割積分でも、一般的な使用目的であれば、問題ない精度でしょう。
プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, VclTee.TeeGDIPlus, VCLTee.TeEngine, VCLTee.Series,
Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart, Vcl.StdCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Chart1: TChart;
Series1: TLineSeries;
Series2: TLineSeries;
Series3: TLineSeries;
Series4: TLineSeries;
Series5: TLineSeries;
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
Memo1: TMemo;
Label1: TLabel;
Label2: TLabel;
Series6: TLineSeries;
Image1: TImage;
procedure Button1Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
private
{ Private 宣言 }
function fy(a, b, x: double): boolean;
procedure Linedraw;
procedure Textdraw;
procedure area;
procedure second_imperfect_elliptic_integral(z, K: double; var F, E: Double);
procedure arch;
procedure archoutdraw;
procedure integral;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
uses math;
var
a, b : double;
x, y : double;
xp : integer;
stb, ltb, mtb: string;
procedure TForm1.Button1Click(Sender: TObject);
var
ch : integer;
begin
// a := 3;
// b := 3;
// x := 4;
val(LabeledEdit1.Text, a, ch);
if ch <> 0 then begin
application.MessageBox('aの値に間違いがあります。','注意',0);
exit;
end;
if a <= 0 then begin
application.MessageBox('aの値はゼロより大きくして下さい。','注意',0);
exit;
end;
val(LabeledEdit2.Text, b, ch);
if ch <> 0 then begin
application.MessageBox('bの値に間違いがあります。','注意',0);
exit;
end;
if b <= 0 then begin
application.MessageBox('bの値はゼロより大きくして下さい。','注意',0);
exit;
end;
val(LabeledEdit3.Text, x, ch);
if ch <> 0 then begin
application.MessageBox('Xの値に間違いがあります。','注意',0);
exit;
end;
if not fy(a, b, x) then
application.MessageBox('Xの値は、aの値より大きくなくてはいけません。','注意',0);
end;
// 弓形部,扇形部の面積、長さの分割積分確認計算
procedure TForm1.integral;
var
i, n : integer;
dx, s, y0, y1, ax, L, ss: double;
st, su : string;
ch0, ch1 : char;
En : integer;
begin
s := 0;
dx := (x - a) / 1000; // Δx'
n := round((x - a) / dx); // 分割数
dx := (x - a) / n; // Δx
L := 0;
ax := a; // 中間点で計算
y0 := b / a * sqrt(ax * ax - a * a); // yの値計算
for i := 1 to n do begin
ax := dx * i + a;
y1 := b / a * sqrt(ax * ax - a * a); // yの値計算
s := s + (y0 + y1) * dx; // 面積 (y0+y0)は両サイド
L := L + sqrt((y1 - y0) * (y1 - y0) + dx * dx);
y0 := y1;
end;
ss := y0 * x - s; // 扇部面積
memo1.Lines.Add('');
st := floatTostr(s); // 弓形部面積の文字変換
su := '';
n := length(st); // 文字長さ
En := n;
for i := 1 to n do begin // 指数部検索
if stb[i] = 'E' then En := i;
end;
for i := 1 to n do begin // 上の桁から一致する桁だけ取り出し
ch0 := stb[i];
ch1 := st[i];
if ch0 = ch1 then su := su + ch0
else break;
end;
if su <> '' then
for i := En to n do begin // 指数部加算
ch0 := stb[i];
su := su + ch0;
end;
if su = '' then su := floattostr(s);
memo1.Lines.Add('分割積分確認Su = ' + su);
st := floatTostr(ss); // 扇部面積文字変換
su := '';
n := length(st); // 文字長さ
En := n;
for i := 1 to n do begin // 指数部検索
if mtb[i] = 'E' then En := i;
end;
for i := 1 to n do begin // 上の桁から一致する桁だけ取り出し
ch0 := mtb[i];
ch1 := st[i];
if ch0 = ch1 then su := su + ch0
else break;
end;
if su <> '' then
for i := En to n do begin // 指数部加算
ch0 := mtb[i];
su := su + ch0
end;
if su = '' then su := floattostr(ss);
memo1.Lines.Add('分割積分確認So = ' + su);
st := floatTostr(L); // 双曲弧の長さ文字変換
su := '';
n := length(st); // 文字長さ
En := n;
for i := 1 to n do begin // 指数部検索
if ltb[i] = 'E' then En := i;
end;
for i := 1 to n do begin // 上の桁から一致する桁だけ取り出し
ch0 := ltb[i];
ch1 := st[i];
if ch0 = ch1 then su := su + ch0
else break;
end;
if su <> '' then
for i := En to n do begin // 指数部加算
ch0 := ltb[i];
su := su + ch0
end;
if su = '' then su := floattostr(L);
memo1.Lines.Add('分割積分確認 L = ' + su);
end;
//-------------------------------
// 第1種第2種楕円積分
// FBnKn[0] 第1種楕円積分解
// EBnKn[0] 第2種楕円積分解
// ランデン変換
// Q 角度 deg
// K 離心率
//-------------------------------
procedure TForm1.second_imperfect_elliptic_integral(z, K: double; var F, E: Double);
var
I, MI : integer;
Kn : array of double; // Kn
knd : array of double; // k'n
N2SKn : array of double; // 2/(1+Kn)
T2SKnd : array of double; // П2/(1+Kn')
BRad : array of double; // β(rad)
SinBn : array of double; // sinβn
FBnKn : array of double; // F(βn,kn)
EBnKn : array of double; // E(βn,kn)
LnD : double;
Q : double;
begin
// K = 0 の時は円なのでpiの角度値radをかえします。
Q := arcsin(z);
if K = 0 then begin
E := Q;
F := E;
exit;
end;
// この時は1をかえします 演算エラー防止の為、値は正しくありません。
if (K = 1) and (Q >= pi / 2) then begin
E := 1;
F := 1;
exit;
end;
// (1 > K > 0 and Q <= 90°) or (K = 1 and Q < 90°)の時
MI := 0;
LND := 0;
setlength(kn, MI + 1); // kn
kn[0] := K;
while LND <> Kn[MI] do begin
LnD := Kn[MI];
inc(MI);
setlength(kn, MI + 1); // kn
kn[MI] := 2 * sqrt(Kn[MI - 1])/(1 + Kn[MI - 1]);
end;
Dec(MI);
setlength(kn, MI + 1); // kn
setlength(knd, MI + 1); // k'n
setlength(N2SKn, MI + 1); // 2/(1+Kn)
setlength(T2SKnd, MI + 1); // П2/(1+Kn')
setlength(BRad, MI + 1); // β(rad)
setlength(SinBn, MI + 1); // sinβn
setlength(FBnKn, MI + 1); // F(βn,kn)
setlength(EBnKn, MI + 1); // E(βn,kn)
knd[0] := 1;
for I := 1 to MI do
knd[I] := (1 - kn[I - 1]) / (1 + Kn[I - 1]);
for I := 0 to MI do
N2SKn[I] := 2 / (1 + kn[I]);
T2SKnd[MI] := N2SKn[MI];
for I := MI - 1 downto 0 do
T2SKnd[I] := T2SKnd[I + 1] * N2SKn[I];
BRad[0] := Q;
for I := 1 to MI do
BRad[I] := (arcsin(kn[I - 1] * sin(Brad[I - 1])) + Brad[I - 1]) / 2;
for I := 0 to MI do
SinBn[I] := sin(Brad[I]);
LnD := LN((1 + sin(Brad[MI])) / cos(Brad[MI]));
for I := 0 to MI do
FBnKn[I] := T2SKnd[I] * LnD;
F := FBnKn[0];
EBnKn[MI] := sin(Brad[MI]);
for I := MI - 1 downto 0 do
EBnKn[I] := (2 * EBnKn[I + 1] + 2 * knd[I + 1] * FBnKn[I + 1]) / (1 + knd[I + 1]) - kn[I] * SinBn[I];
E := EBnKn[0];
end;
// 扇形部の塗りつぶし
procedure TForm1.archoutdraw;
var
i, kn : integer;
Xbase, Ybase : integer;
Xn, Yn, yni : integer;
Yx : double;
ax, ay : double;
dx, px : double;
py : double;
begin
Image1.Canvas.Pen.Color := clSkyblue; // 色空色
Image1.Canvas.Pen.Width := 1;
Image1.Canvas.Pen.Style := psSolid;
Xbase := Series2.CalcXPos(1); // 原点位置座標 X
Ybase := Series2.CalcYPos(1); // 原点位置座標 y
Xn := Series1.CalcXPos(xp); // X位置x座標
Yn := Series1.CalcYPos(xp); // Y位置y座標
Image1.Canvas.MoveTo(Xbase, Ybase); // 境界線の描画
Image1.Canvas.LineTo(Xn, Yn);
Yn := Series3.CalcYPos(xp);
Image1.Canvas.MoveTo(Xbase, Ybase);
Image1.Canvas.LineTo(Xn, Yn);
ax := (Xn - Xbase) / x; // xに対するX座標の変化率
y := b / a * sqrt(x * x - a * a); // 双曲線yの値
ay := (Yn - Ybase) / y; // yに対するY座標の変化率
kn := round((Xn - Xbase) / 5); // 0~X迄の分割数
dx := x / kn; // Δx
for i := 0 to kn do begin // 塗りつぶし線の描画
px := i * dx;
py := y / x * px;
Xn := round(ax * px) + Xbase;
if px < a then begin // aの値までは上の境界から下の境界まで
Yn := round(ay * py) + Ybase;
Image1.Canvas.MoveTo(Xn, Yn);
Yn := - round(ay * py) + Ybase;
Image1.Canvas.LineTo(Xn, Yn);
end
else begin // aの値を超えたら双曲範囲を避けて描画
Yn := round(ay * py) + Ybase;
Yx := b / a * sqrt(px * px - a * a);
yni := Ybase + round(ay * Yx);
Image1.Canvas.MoveTo(Xn, Yn);
Image1.Canvas.LineTo(Xn, Yni);
Yn := - round(ay * py) + Ybase;
yni := Ybase - round(ay * Yx);
Image1.Canvas.MoveTo(Xn, Yn);
Image1.Canvas.LineTo(Xn, Yni);
end;
end;
end;
// 双曲弧の長さ計算
// L 双曲弧の長さの二分の一
procedure TForm1.arch;
var
e, k, z : double;
Fzk, Ezk : double;
L : double;
begin
e := sqrt(a * a + b * b) / a; // 離心率e
memo1.Lines.Add('離心率 e = ' + floatTostr(e));
k := 1 / e; // k
z := sqrt((x * x - a * a) / (x * x - k * k * a * a)); // z
second_imperfect_elliptic_integral(z, k, Fzk, Ezk); // 第一種第二種楕円積分
L := (a * (1 - k * k) * Fzk - a * Ezk + x * z) / k; // L
ltb := floatTostr(L);
memo1.Lines.Add('双曲弧の長さ L = ' + ltb);
end;
// 双曲線 弓形部と扇形部の面積の面積
procedure TForm1.area;
var
y, s, so: double;
begin
memo1.Clear;
y := b / a * sqrt(x * x - a * a); // y
s := x * y - a * b * arccosh(x / a); // s 弓形部の面積
stb := floatTostr(s);
memo1.Lines.Add('弓形部の面積 Su = ' + stb);
so := a * b * arccosh(x / a); // so 扇形部の面積
mtb := floatTostr(so);
memo1.Lines.Add('扇形部の面積 So = ' + mtb);
end;
// TChartに文字出力
procedure TForm1.Textdraw;
var
xpp, ypp: integer;
begin
Image1.Canvas.Font.Size := 15; // 文字の高さSize(integer)ではだめ
Image1.Canvas.Font.Color := clRed;
Image1.Canvas.Font.Name := 'Tahoma';
xpp := (Series2.CalcXPos(1) + Series1.CalcXPos(0)) div 2; // 文字aのx位置計算
ypp := Series2.CalcyPos(1) - 4; // 文字aのy位置計算
Image1.Canvas.TextOut(xpp, ypp, 'a'); // aの描画
xpp := Series1.CalcXPos(0) - 14; // 文字bのx位置計算
ypp := Series1.CalcYPos(0) - ((Series1.CalcYPos(0) - Series2.CalcYPos(2)) div 2) - 10; // 文字bのy位置計算
Image1.Canvas.TextOut(xpp, ypp, 'b'); // bの描画
xpp := (Series2.CalcXPos(1) + Series2.CalcXPos(2)) div 2 - 12; // 文字cのx位置計算
ypp := (Series2.CalcYPos(1) + Series2.CalcYPos(2)) div 2 - 25; // 文字cのy位置計算
Image1.Canvas.TextOut(xpp, ypp, 'c'); // cの描画
Image1.Canvas.Font.Color := clblack;
xpp := Series5.CalcXPos(0) - 17; // 文字xのx位置計算
ypp := Series2.CalcYPos(3) - 25; // 文字xのy位置計算
Image1.Canvas.TextOut(xpp, ypp, 'x'); // xの描画
xpp := Series1.CalcXPos(0) + 17; // 文字Lのx位置計算
ypp := Series1.CalcYPos(0) + ((Series3.CalcYPos(xp) - Series1.CalcYPos(0)) div 2) - 17; // 文字Lのy位置計算
Image1.Canvas.TextOut(xpp, ypp, 'L'); // Lの描画
end;
// 直線の描画
procedure TForm1.Linedraw;
var
i : integer;
xp1, yp1: integer;
xp2, yp2: integer;
begin
xp1 := Series1.CalcXPos(0); // 双曲線原点X
yp1 := Series1.CalcYPos(0); // 双曲線原点y
xp2 := Series2.CalcXPos(2); // y=b/a * b の x座標 xp1と同じ
yp2 := Series2.CalcYPos(2); // y=b/a * b の y座標
Image1.Canvas.Pen.Color := clBlue;
Image1.Canvas.Pen.Width := 3;
Image1.Canvas.Pen.Style := psSolid;
Image1.Canvas.MoveTo(xp1,yp1); // b の線
Image1.Canvas.LineTo(xp2,yp2);
xp2 := Series2.CalcXPos(1); // x=0 の座標
yp2 := Series2.CalcyPos(1); // y=0 の座標
Image1.Canvas.LineTo(xp2,yp2); // c の線 三角形斜線
Image1.Canvas.Pen.Color := clGreen;
Image1.Canvas.Pen.Width := 3;
Image1.Canvas.Pen.Style := psSolid;
for i := 0 to xp do begin // 双曲線弓形部塗りつぶし
if i mod 2 = 0 then begin
xp1 := Series1.CalcXPos(i);
yp1 := Series1.CalcYPos(i);
xp2 := Series3.CalcXPos(i);
yp2 := Series3.CalcYPos(i) - 2; // LのRedLineを避けます
Image1.Canvas.MoveTo(xp1,yp1);
Image1.Canvas.LineTo(xp2,yp2);
end;
end;
Image1.Canvas.Pen.Color := clblack;
Image1.Canvas.Pen.Width := 1;
Image1.Canvas.Pen.Style := psDashdotdot;
xp1 := Series2.CalcXPos(0);
xp2 := Series2.CalcXPos(4);
yp1 := Series4.CalcYPos(1);
yp2 := Series4.CalcYPos(1);
Image1.Canvas.MoveTo(xp1,yp1); // X軸線
Image1.Canvas.LineTo(xp2,yp2);
xp1 := Series2.CalcXPos(1);
xp2 := Series2.CalcXPos(1);
yp1 := Series5.CalcYPos(0);
yp2 := Series5.CalcYPos(1);
Image1.Canvas.MoveTo(xp1,yp1); // y軸線
Image1.Canvas.LineTo(xp2,yp2);
xp1 := Series2.CalcXPos(1);
xp2 := Series1.CalcXPos(0);
yp1 := Series2.CalcYPos(1);
yp2 := Series1.CalcYPos(0);
Image1.Canvas.Pen.Style := psSolid;
Image1.Canvas.Pen.Width := 3;
Image1.Canvas.MoveTo(xp1,yp1); // aの線
Image1.Canvas.LineTo(xp2,yp2);
end;
// 双曲線の描画
function TForm1.fy(a, b, x: double): boolean;
const
nk100 = 100; // 双曲線分割数
var
i : integer;
dx, ax: double;
Xmax, Xmin, ymax : double;
begin
if a >= x then begin // a < x の確認
result := false;
exit;
end;
result := true;
Image1.Canvas.Brush.Style := bsSolid;
Image1.Canvas.FillRect(rect(0, 0, Image1. Width, Image1. Height));
Image1.Canvas.Brush.Style := bsClear;
Chart1.BackImage.Bitmap := Image1.Picture.Bitmap;
Series1.Clear; // 双曲線+側
Series2.Clear; // y = a/b * x
Series3.Clear; // 双曲線-側
Series4.Clear; // y = -a/b * x
Series5.Clear; // xの位置
Series6.Clear; // Lの線
xp := 0; // 双曲線Series1がXの値になる配列の位置 クリア
dx := (x * 1.5 - a) / nk100; // 双曲線計算のΔx
ymax := b / a * sqrt(x * x * 1.5 * 1.5 - a * a); // y軸最大値 最小値-ymax
Xmax := x * 1.5; // x軸最大値
Xmin := -x / 2; // x軸最小値
// TChartのXY軸計算
// Maximum > Minimum の条件を守る為、現在の値と、新しくセットする値で順番設定
// X軸とY軸のスケールを同じに設定します
if ymax > (Xmax - Xmin) / 2 then begin
if Chart1.LeftAxis.Maximum < ymax then begin
Chart1.LeftAxis.Maximum := ymax;
Chart1.LeftAxis.Minimum := -ymax;
end
else begin
Chart1.LeftAxis.Minimum := -ymax;
Chart1.LeftAxis.Maximum := ymax;
end;
if Chart1.BottomAxis.Maximum < ymax * 2 + Xmin then begin
Chart1.BottomAxis.Maximum := ymax * 2 + Xmin;
Chart1.BottomAxis.Minimum := Xmin;
end
else begin
Chart1.BottomAxis.Minimum := Xmin;
Chart1.BottomAxis.Maximum := ymax * 2 + Xmin;
end;
end
else begin
ymax := (Xmax - Xmin) / 2;
if Chart1.LeftAxis.Maximum < ymax then begin
Chart1.LeftAxis.Maximum := ymax;
Chart1.LeftAxis.Minimum := -ymax;
end
else begin
Chart1.LeftAxis.Minimum := -ymax;
Chart1.LeftAxis.Maximum := ymax;
end;
if Chart1.BottomAxis.Maximum < Xmax then begin
Chart1.BottomAxis.Maximum := Xmax;
Chart1.BottomAxis.Minimum := Xmin;
end
else begin
Chart1.BottomAxis.Minimum := Xmin;
Chart1.BottomAxis.Maximum := Xmax;
end;
end;
// 双曲線グラフ作図
for i := 0 to nk100 do begin
ax := a + i * dx; // 双曲線xの値
if ax <= x then xp := i; // 双曲線Series1がXの値になる配列の位置
y := b / a * sqrt(ax * ax - a * a); // 双曲線yの値
if ax <= x then Series6.AddXY(ax, -y);; // Lの範囲グラフ
Series1.AddXY(ax, y); // +双曲線
Series3.AddXY(ax, -y); // -双曲線
end;
// y = b/a * x, -y の直線グラフ, Xの位置の直線
dx := -a / 5;
y := b / a * dx;
Series2.AddXY(dx, y); // 最初の位置 双曲線 基準線 y = b/a * x Series(0)
Series4.AddXY(dx, -y); // -y
dx := 0;
y := 0;
Series2.AddXY(dx, y); // ゼロの位置 双曲線 基準線 y = b/a * x Series(1)
Series4.AddXY(dx, -y); // -y
dx := a;
y := b / a * dx;
Series2.AddXY(dx, y); // aの位置 双曲線 基準線 y = b/a * x Series(2)
Series4.AddXY(dx, -y); // -y
dx := x;
y := b / a * dx;
Series2.AddXY(dx, y); // xの位置 双曲線 基準線 y = b/a * x Series(3)
Series4.AddXY(dx, -y); // -y
dx := x * 1.5;
y := b / a * dx;
Series2.AddXY(dx, y); // x*1.5の位置 双曲線 基準線 y = b/a * x Series(4)
Series4.AddXY(dx, -y); // -y
y := ymax;
Series5.AddXY(x, -y); // Xの位置の垂直線-y
Series5.AddXY(x, y); // Xの位置の垂直線 y
Chart1.Update;
application.ProcessMessages; // Chart1グラフ描画待ち
archoutdraw;
Linedraw; // 直線描画
application.ProcessMessages;
Textdraw; // 文字描画
area; // 弓形部の面積の面積
arch; // 双曲弧の長さ計算
application.ProcessMessages;
integral; // 分割積分による確認
Chart1.BackImage.Bitmap := Image1.Picture.Bitmap;
Memo1.Lines.Add('弓形部 緑色');
Memo1.Lines.Add('扇形部 空色');
end;
procedure TForm1.FormCreate(Sender: TObject);
var
bm : Tbitmap;
begin
bm := Tbitmap.Create;
bm.Width := Chart1.Width;
bm.Height := Chart1.Height;
Image1.Width := Chart1.Width;
Image1.Height := Chart1.Height;
Image1.Picture.Bitmap := bm;
Image1.Canvas.Brush.Color := clWhite;
Image1.Visible := False;
bm.free;
end;
end.