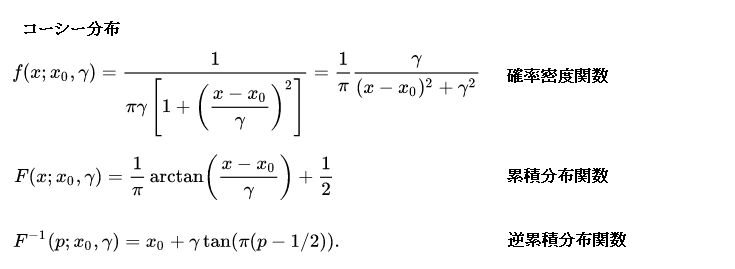
コーシー、ロジスティック、指数分布
コーシー、ロジスティック、指数分布の各分布の計算は、簡単な計算なので、一つにまとめてみました。
各分布の内容や使用法については、インターネットで検索して下さい。
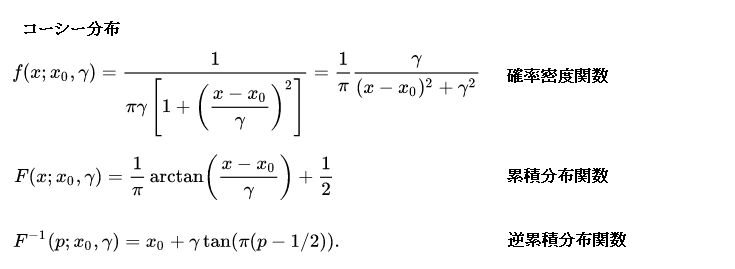
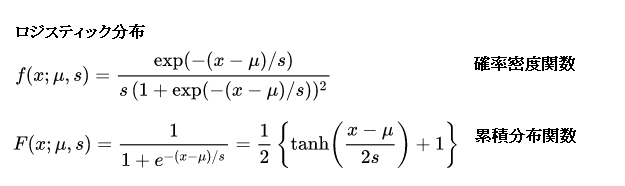

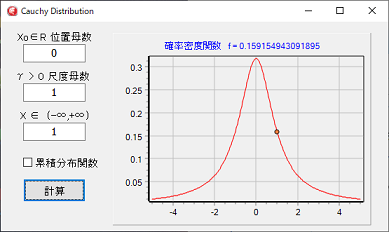
コーシー分布プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, system.Math, VclTee.TeeGDIPlus,
VCLTee.Series, VCLTee.TeEngine, Vcl.ExtCtrls, VCLTee.TeeProcs, VCLTee.Chart,
Vcl.StdCtrls, Vcl.Buttons;
type
TForm1 = class(TForm)
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
BitBtn1: TBitBtn;
CheckBox1: TCheckBox;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
procedure BitBtn1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
//---------------- Cauchy distribution ----------------------------
// x 位置
// x0 平均値(中央値)
// g γ 正規分布のσと同じで意味の分散値
//-----------------------------------------------------------------
// 確率密度
function Probability(x, x0, g: double): double;
begin
result := g / (sqr(x - x0) + sqr(g)) / pi;
end;
// 累積分布(下側)
function Cumulative(x, x0, g: double): double;
begin
result := arctan((x - x0) / g) / pi + 1 / 2;
end;
// 累積分布逆計算
// 累積分布の値pからX位置の値を求めます。
function arcCumulative(p, x0, g: double): double;
begin
result := x0 + g * tan(pi * (p - 1 /2));
end;
// 計算
procedure TForm1.BitBtn1Click(Sender: TObject);
const
n = 200;
var
ch: integer;
x0, x, g: double;
f, fb: double;
xmin, xmax, dx: double;
col: Tcolor;
begin
val(Labelededit1.Text, x0, ch);
if ch <> 0 then begin
application.MessageBox('Xoの値に間違いがあります。','注意',0);
exit;
end;
val(Labelededit2.Text, g, ch);
if ch <> 0 then begin
application.MessageBox('γの値に間違いがあります。','注意',0);
exit;
end;
val(Labelededit3.Text, x, ch);
if ch <> 0 then begin
application.MessageBox('Xの値に間違いがあります。','注意',0);
exit;
end;
Series1.Clear;
Series2.Clear;
chart1.Title.Text.Clear;
if checkbox1.Checked = false then begin
f := Probability(x, x0, g);
chart1.Title.Text.Add('確率密度関数 f = ' + floatTostr(f));
col := clRed;
Series2.AddXY(x, f);
end
else begin
f := Cumulative(x, x0, g);
chart1.Title.Text.Add('累積分布関数 F = ' + floatTostr(f));
fb := arcCumulative(f, x0, g); // 累積分布逆計算 検算
col := clblue;
Series2.AddXY(fb, f);
end;
xmin := -5;
xmax := 5;
if x < xmin + 1 then xmin := x - 1;
if x > xmax - 1 then xmax := x + 1;
dx := (xmax - xmin) / n;
for ch := 0 to n do begin
x := ch * dx + xmin;
if checkbox1.Checked = false then f := Probability(x, x0, g)
else f := Cumulative(x, x0, g);
Series1.AddXY(x, f, '', col);
end;
end;
end.
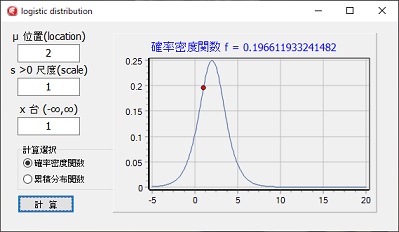
ロジスティック分布プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, system.Math, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.Series, VCLTee.TeEngine, VCLTee.TeeProcs,
VCLTee.Chart, Vcl.Buttons, system.UITypes;
type
TForm1 = class(TForm)
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
RadioGroup1: TRadioGroup;
BitBtn1: TBitBtn;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
Series3: TFastLineSeries;
procedure BitBtn1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
// ロジスティック分布
//------------ 累積分布関数 -----------------------------
// x 台(-∞,∞)
// u 位置(location)
// s >0 尺度(scale)
//-------------------------------------------------------
function Logistic_Distribution(x, u, s: double): double;
begin
if s <=0 then begin
result := 0;
exit;
end;
result := (tanh((x - u) / 2 / s) + 1) / 2;
end;
//------------ 確率密度関数 -----------------------------
// x 台(-∞,∞)
// u 位置(location)
// s >0 尺度(scale)
//-------------------------------------------------------
function Logistic_Density(x, u, s: double): double;
var
umx, a, b: double;
begin
if s <=0 then begin
result := 0;
exit;
end;
umx := (u - x) / s;
a := exp(umx);
b := 1 + exp(umx);
b := s * b * b;
result := a / b;
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
const
n = 200;
var
u, s, x: double;
dx, xx, f: double;
ch : integer;
min, max: double;
begin
val(labelededit1.Text, u, ch);
if ch <> 0 then begin
MessageDlg('μ位置に間違いがあります。', mtWarning, [mbOk], 0, mbOk);
exit;
end;
val(labelededit2.Text, s, ch);
if ch <> 0 then begin
MessageDlg('s 尺度に間違いがあります。', mtWarning, [mbOk], 0, mbOk);
exit;
end;
val(labelededit3.Text, x, ch);
if ch <> 0 then begin
MessageDlg('x 台に間違いがあります。', mtWarning, [mbOk], 0, mbOk);
exit;
end;
Chart1.Title.Clear;
series1.Clear;
series2.Clear;
series3.Clear;
case RadioGroup1.ItemIndex of
0 : begin
f := Logistic_Density(x, u, s);
Chart1.Title.Text.Add('確率密度関数 f = ' + floatTostr(f));
series2.AddXY(x, f);
end;
1 : begin
f := Logistic_Distribution(x, u, s);
Chart1.Title.Text.Add('累積分布関数 F = ' + floatTostr(f));
series2.AddXY(x, f);
end;
end;
min := -5;
max := 20;
if x < min + 1 then min := x - 1;
if x > max - 1 then max := x + 1;
dx := (max - min) / n;
for ch := 0 to n do begin
xx := ch * dx + min;
case RadioGroup1.ItemIndex of
0 : f := Logistic_Density(xx, u, s);
1 : begin
f := Logistic_Distribution(xx, u, s);
if xx < x then begin
series3.AddXY(xx, 0);
series3.AddXY(xx, f);
series3.AddXY(xx, 0);
end;
end;
end;
series1.AddXY(xx, f);
end;
end;
end.
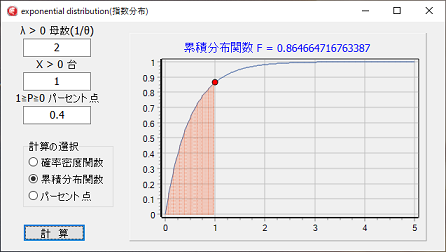
指数分布プログラム
unit Main;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, system.Math, Vcl.StdCtrls, Vcl.ExtCtrls,
VclTee.TeeGDIPlus, VCLTee.Series, VCLTee.TeEngine, VCLTee.TeeProcs,
VCLTee.Chart, Vcl.Buttons, system.UITypes;
type
TForm1 = class(TForm)
LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit;
LabeledEdit3: TLabeledEdit;
RadioGroup1: TRadioGroup;
BitBtn1: TBitBtn;
Chart1: TChart;
Series1: TLineSeries;
Series2: TPointSeries;
Series3: TFastLineSeries;
procedure FormCreate(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
private
{ Private 宣言 }
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
// 指数分布
// --------------- 累積分布関数 ---------------------
// x 台 (0, ∞)
// r 母数 r > 0
//---------------------------------------------------
function Exponential_Distribution(x, r: double): double;
begin
if (x >= 0) and (r > 0) then result := 1 - exp(- x * r)
else result := 0;
end;
//---------------- 確率密度関数----------------------
// x 台 (0, ∞)
// r 母数 r > 0
//---------------------------------------------------
function Exponential_Density(x, r: double): double;
begin
if (x >= 0) and (r > 0) then result := r * exp(- x * r)
else result := 0;
end;
// --------------- 累積分布逆関数 --------------------
// p パーセント点 0~1
// r 母数 r > 0
//----------------------------------------------------
function arcExponential_Distribution(p, r: double): double;
begin
if p >= 1 then begin
result := infinity;
exit;
end;
if (p < 1) and (p >= 0) and (r > 0) then begin
result := ln(1 - p);
result := - result / r;
end
else result := 0;
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
const
n = 200;
var
x, r, p: double;
dx, xx: double;
ch : integer;
f : double;
max : double;
begin
f := 0;
x := 0;
p := 0;
val(labelededit1.Text, r, ch);
if ch <> 0 then begin
MessageDlg('λ母数に間違いがあります。', mtWarning, [mbOk], 0, mbOk);
exit;
end;
if (RadioGroup1.ItemIndex = 0) or (RadioGroup1.ItemIndex = 1) then begin
val(labelededit2.Text, x, ch);
if ch <> 0 then begin
MessageDlg('X 台に間違いがあります。', mtWarning, [mbOk], 0, mbOk);
exit;
end;
end;
if RadioGroup1.ItemIndex = 2 then begin
val(labelededit3.Text, p, ch);
if ch <> 0 then begin
MessageDlg('P パーセント点に間違いがあります。', mtWarning, [mbOk], 0, mbOk);
exit;
end;
end;
Chart1.Title.Clear;
series1.Clear;
series2.Clear;
series3.Clear;
case RadioGroup1.ItemIndex of
0 : begin
f := Exponential_Density(x, r);
Chart1.Title.Text.Add('確率密度関数 f = ' + floatTostr(f));
series2.AddXY(x, f);
end;
1 : begin
f := Exponential_Distribution(x, r);
Chart1.Title.Text.Add('累積分布関数 F = ' + floatTostr(f));
series2.AddXY(x, f);
end;
2 : begin
x := arcExponential_Distribution(p, r);
Chart1.Title.Text.Add('パーセント点 x = ' + floatTostr(x));
if x < maxsingle then series2.AddXY(x, p);
end;
end;
max := 5;
if x = infinity then exit;
if x > max - 1 then max := x + 1;
dx := max / n;
for ch := 0 to 200 do begin
xx := ch * dx;
case RadioGroup1.ItemIndex of
0 : f := Exponential_Density(xx, r);
1,2 : begin
f := Exponential_Distribution(xx, r);
if xx < x then begin
series3.AddXY(xx, 0);
series3.AddXY(xx, f);
series3.AddXY(xx, 0);
end;
end;
end;
series1.AddXY(xx, f);
end;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
with RadioGroup1 do begin
Items.Add('確率密度関数');
Items.Add('累積分布関数');
Items.Add('パーセント点');
ItemIndex := 0;
end;
end;
end.
logistic_distribution.zip の中に3個のプログラムが入っています。
![]() logistic_distribution.zip
logistic_distribution.zip