カールソンの楕円積分(複素数)Ｎｏ２

　バリアントの複素数でのRC,RF,RJのプログラムが出来たので、それを出来る限りＤｏｕｂｌｅでの複素数に変更してみます。

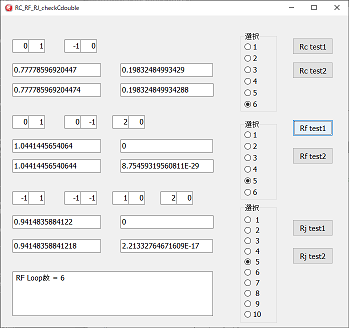　Doubleの計算なので、有効桁数17桁程度なので、ゼロの値が最大で17桁目がゼロにならない事があります。
Variantの複素数の場合は、小数点以下12桁目より小さい値はゼロになりますが、複素数での関数演算は、Extendedより多い有効桁数で計算するので、計算によっては、Doubleより精度が高くなるようです。
しかし、演算をソフトルーチンで行なう為、非常に遅くなります。
左図プログラム例では、RJの３のパターンで、Variantの複素数の計算と、Doubleでの複素数の計算では１２桁目辺りに差が出ます。
その差は、RCの複素数の平方根によるもので、RJの計算の場合、RCの計算結果の∑値を計算するので、僅かな誤差が積み重なって、誤差が大きくなります。
　Doubleではなく、Extendedで計算すれば、問題のない誤差となります。
しかし、６４ビット対応を考えると、四則演算以外はＶａｒｉａｎｔの関数を使用するのが良いようです。

// 1/31/2021
// プログラムは https://arxiv.org/abs/math/9409227　のレポートを元に作成しています

unit Main;

interface

uses
  Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
  Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls, Vcl.Buttons;

type
  TForm1 = class(TForm)
    Memo1: TMemo;
    RJtest1: TBitBtn;
    Rjdtxr: TEdit;
    Rjdtyr: TEdit;
    Rjdtzr: TEdit;
    Rjdtpr: TEdit;
    Rjansr: TEdit;
    Rjansi: TEdit;
    Rjclc0: TEdit;
    Rjclc1: TEdit;
    RjRadio: TRadioGroup;
    Rjdtxi: TEdit;
    Rjdtyi: TEdit;
    Rjdtzi: TEdit;
    Rjdtpi: TEdit;
    Rjtest2: TBitBtn;
    Rftest1: TBitBtn;
    Rftest2: TBitBtn;
    Rctest1: TBitBtn;
    Rctest2: TBitBtn;
    Rfdtxr: TEdit;
    Rfdtxi: TEdit;
    Rfdtyr: TEdit;
    Rfdtyi: TEdit;
    Rfdtzr: TEdit;
    Rfdtzi: TEdit;
    Rfansr: TEdit;
    Rfansi: TEdit;
    Rfclc0: TEdit;
    Rfclc1: TEdit;
    RfRadio: TRadioGroup;
    Rcdtxr: TEdit;
    Rcdtxi: TEdit;
    Rcdtyr: TEdit;
    Rcdtyi: TEdit;
    Rcclc0: TEdit;
    Rcclc1: TEdit;
    Rcansi: TEdit;
    Rcansr: TEdit;
    RcRadio: TRadioGroup;
    procedure RJtest1Click(Sender: TObject);
    procedure Rjtest2Click(Sender: TObject);
    procedure Rftest1Click(Sender: TObject);
    procedure Rftest2Click(Sender: TObject);
    procedure Rctest1Click(Sender: TObject);
    procedure Rctest2Click(Sender: TObject);
  private
    { Private 宣言 }
  public
    { Public 宣言 }
  end;

var
  Form1: TForm1;

implementation

{$R *.dfm}

uses system.Math, System.VarCmplx, mp_types, mp_real, mp_cmplx;

// 複素数の生成
function Varcomplex(a, b: double): Variant;
begin
  result := varascomplex(result);
  result.real := a;
  result.Imaginary := b;
end;

// 複素数構造体
type
  TCdouble = record
    r : double;
    i : double;
  end;

// 複素数の生成
function Vc(a, b: double): TCdouble;
begin
  result.r := a;
  result.i := b;
end;

// 複素数変換  Varint to TCdouble
function VtoT(x : variant): TCdouble;
begin
  result.r := x.real;
  result.i := x.Imaginary;
end;

// 複素数変換  TCdouble to variant
function TtoV(x : TCdouble): variant;
begin
  result := varascomplex(result);
  result.real := x.r;
  result.Imaginary := x.i;
end;

// TCdouble複素数の生成
{VCと同じです}
function MCdouble(r, i: double): TCdouble;
begin
  result.r := r;
  result.i := i;
end;

// TCdouble複素数の加算
function cadd(a, b: TCdouble): TCdouble;
begin
  result.r := a.r + b.r;
  result.i := a.i + b.i;
end;

// TCdouble複素数の減算
function csub(a, b: TCdouble): TCdouble;
begin
  result.r := a.r - b.r;
  result.i := a.i - b.i;
end;

// TCdouble複素数の乗算
function cmul(a, b: TCdouble): TCdouble;
begin
  result.r := a.r * b.r - a.i * b.i;
  result.i := a.r * b.i + a.i * b.r;
end;

// TCdouble複素数とDoubleの乗算
function cmuld(a: TCdouble;  b: double): TCdouble;
begin
  result.r := a.r * b;
  result.i := a.i * b;
end;

// TCdouble複素数とDoubleの除算
function cdivd(a: TCdouble;  b: double): TCdouble;
begin
  result.r := a.r / b;
  result.i := a.i / b;
end;

// TCdouble複素数の除算
function cdiv(a, b: TCdouble): TCdouble;
var
  bb: double;
begin
  result.r := 0;
  result.i := 0;
  bb := b.r * b.r + b.i * b.i;
  if bb <> 0 then begin
    result.r := (a.r * b.r + a.i * b.i) / bb;
    result.i := (a.i * b.r - a.r * b.i) / bb;
  end;
end;

// TCdouble複素数の符号反転
function cchs(a: TCdouble): TCdouble;
begin
  result.r := -a.r;
  result.i := -a.i;
end;

// 複素数の平方根
function csqrt(x: TCdouble): TCdouble;
var
  len: double;
begin
  len := sqrt(x.r * x.r + x.i * x.i);
  result.r := sqrt((len + x.r) / 2);
  result.i := sqrt((len - x.r) / 2);
  if x.i < 0 then result.i := -result.i;
end;

// 複素数の平方根 variant                 {Doubleの複素数TCdoubleからVariantの複素数に変換しルート計算後TCdoubleに戻しています}
function tsqrt(x: TCdouble): TCdouble;
var
  xv, xs : variant;
begin
  xv := varcomplex(x.r, x.i);
  xs := varcomplexsqrt(xv);
  result := MCdouble(xs.real, xs.imaginary);
end;

// 複素数の平方根 多倍長                  {Doubleの複素数TCdoubleから多倍長の複素数に変換しルート計算後TCdoubleに戻しています}
function asqrt(x: TCdouble): TCdouble;
var
  b, c: mp_complex;
begin
  mpc_init2(b, c);

  mpc_set_dbl(b, x.r, x.i);
  mpc_sqrt(b, c);
  result.r := mpf_todouble(c.re);
  result.i := mpf_todouble(c.im);

  mpc_clear2(b, c);
end;

// a^x　variant
function tpower(x: TCdouble; p : double): TCdouble;
var
  xv, xs : variant;
begin
  xv := varcomplex(x.r, x.i);
  xs := varcomplexpower(xv, p);
  result := MCdouble(xs.real, xs.Imaginary);
end;

// 複素数の絶対値
function cabs(x: TCdouble): double;
var
  a : double;
begin
  a := x.r * x.r + x.i * x.i;
  result := sqrt(a);
end;

// RC
function RCd(x, y: TCdouble): TCdouble;
label
  Ext;
const
  r  = 1E-24;
  c1d = 3 / 10;
  c2d = 1 / 7;
  c3d = 3 / 8;
  c4d = 9 / 22;
  c5d = 159 / 208;
  c6d = 9 / 8;
var
  xt, yt      : TCdouble;
  lamda, Am   : TCdouble;
  A0, s, yb   : TCdouble;
  one, p4, w  : TCdouble;
  c1, c2, c3, c4, c5, c6 : TCdouble;
  d2          : TCdouble;
  tmp         : TCdouble;
  Q           : Double;
  m           : integer;
begin
  if cabs(y) = 0 then begin
    result := MCdouble(0, 0);
    m := 0;
    goto Ext;
  end;

  one := MCdouble(1, 0);
  c1  := MCdouble(c1d, 0);
  c2  := MCdouble(c2d, 0);
  c3  := MCdouble(c3d, 0);
  c4  := MCdouble(c4d, 0);
  c5  := MCdouble(c5d, 0);
  c6  := MCdouble(c6d, 0);
  d2  := MCdouble(2, 0);
  if (y.r > 0) or (y.i <> 0) then begin
    xt := x;
    yt := y;
    w  := MCdouble(1, 0);
  end
  else begin
    xt := csub(x, y);
    yt := cchs(y);
    w := tsqrt(cdiv(x, xt));
  end;
  yb := yt;
  A0 := cdivd(cadd(xt,cadd(yt, yt)), 3);
  Am := A0;
  Q := 1 / power(3 * r, 1 / 8) * cabs(csub(A0, xt));
  m := 0;
  repeat
    lamda := cadd(cmul(d2, cmul(tsqrt(xt), tsqrt(yt))), yt);
    xt := cdivd(cadd(xt, lamda), 4);
    yt := cdivd(cadd(yt, lamda), 4);
    Am := cdivd(cadd(Am, lamda), 4);
    inc(m);
  until power(4, -m) * Q < cabs(Am);
  p4 := MCdouble(power(4, m), 0);
  s := cdiv(cdiv(csub(yb, A0), p4), Am);
  tmp := cadd(c5, cmul(s, c6));
  tmp := cadd(c4, cmul(s, tmp));
  tmp := cadd(c3, cmul(s, tmp));
  tmp := cadd(c2, cmul(s, tmp));
  tmp := cadd(c1, cmul(s, tmp));
  tmp := cadd(one, cmul(s,  cmul(s, tmp)));
  result := cdiv(cmul(w, tmp), tsqrt(Am));               // Varcomplexsqrt
  {ここでの複素数の平方根をTCdouble用に用意した平方根計算を使用すると、例題の3で12桁目辺りに誤差が出ます}
  {多倍長の平方根とvariantの平方根は同じ計算結果となるので、ここで用意したTCdouble平方根の計算とは違うようです}
  {TCdoubleの平方根にextendedを使用するとほぼ近い値となるので、variantの複素数は有効桁数が多いようです}
Ext:
  Form1.Memo1.Lines.Append('RC Loop数 = ' + intTostr(m));
end;

// RF
function RFd(x, y, z: TCdouble): TCdouble;
label
  Ext;
const
  r = 1E-20;
  c1d = 1 / 10;
  c2d = 1 / 14;
  c3d = 1 / 24;
  c4d = 3 / 44;
var
  one             : TCdouble;
  lamda           : TCdouble;
  xm, ym, zm      : TCdouble;
  A0, Am          : TCdouble;
  sqrtx, sqrty, sqrtz  : TCdouble;
  m               : integer;
  X0, Y0, Z0      : TCdouble;
  E2, E3          : TCdouble;
  c1, c2, c3, c4  : TCdouble;
  d3, d4, p4, tmp : TCdouble;
  Q               : double;
begin
  m := 0;
  if cabs(x) = 0 then inc(m);
  if cabs(y) = 0 then inc(m);
  if cabs(z) = 0 then inc(m);
  if m > 1 then begin
    m := 0;
    result := MCdouble(0, 0);
    goto Ext;
  end;

  one := MCdouble(1, 0);
  c1 := MCdouble(c1d, 0);
  c2 := MCdouble(c2d, 0);
  c3 := MCdouble(c3d, 0);
  c4 := MCdouble(c4d, 0);
  d3 := MCdouble(3, 0);
  d4 := MCdouble(4, 0);
  xm := x;
  ym := y;
  zm := z;
  A0 := cdiv(cadd(xm, cadd(ym, zm)),d3);
  Am := A0;
  Q := power(3 * r, -1 / 6) * max(cabs(csub(A0, xm)),
                              max(cabs(csub(A0, ym)), cabs(csub(A0, zm))));
  m := 0;
  repeat
    sqrtx := tsqrt(xm);                                  // Varcomplexsqrt
    sqrty := tsqrt(ym);                                  // Varcomplexsqrt
    sqrtz := tsqrt(zm);                                  // Varcomplexsqrt
    lamda := cadd(cmul(sqrtx,(cadd(sqrty, sqrtz))), cmul(sqrty,sqrtz));
    xm := cdivd(cadd(xm, lamda), 4);
    ym := cdivd(cadd(ym, lamda), 4);
    zm := cdivd(cadd(zm, lamda), 4);
    Am := cdivd(cadd(Am, lamda), 4);
    m := m + 1;
  until power(4, -m) * Q < cabs(Am);
  p4 := MCdouble(power(4, m), 0);
  X0 := cdiv(cdiv(csub(A0, x), p4), Am);
  Y0 := cdiv(cdiv(csub(A0, y), p4), Am);
  Z0 := csub(cchs(X0), Y0);
  E2 := csub(cmul(X0, Y0), cmul(Z0, Z0));
  E3 := cmul(X0, cmul(Y0, Z0));
  tmp := csub(one, cmul(c1, E2));
  tmp := cadd(tmp, cmul(c2, E3));
  tmp := cadd(tmp, cmul(E2, cmul(c3, E2)));
  tmp := csub(tmp, cmul(E3,cmul(c4, E2)));
  result := cmul(cdiv(one, tsqrt(Am)), tmp);             // Varcomplexsqrt

Ext:
  Form1.Memo1.Lines.Append('RF Loop数 = ' + intTostr(m));
end;

// 複素数３個の最小値
function minc3d(a, b, c: TCdouble): TCdouble;
var
  tmp : TCdouble;
begin
  if cabs(a) < cabs(b) then tmp := a
                       else tmp := b;
  if cabs(tmp) < cabs(c) then  result := tmp
                         else  result := c;
end;

// 複素数３個の最大値
function maxc3d(a, b, c: TCdouble): TCdouble;
var
  tmp : TCdouble;
begin
  if cabs(a) > cabs(b) then tmp := a
                       else tmp := b;
  if cabs(tmp) > cabs(c) then  result := tmp
                         else  result := c;
end;

// RJ
function RJd(x, y, z, p: TCdouble): TCdouble;
label
  Ext;
const
  r = 1E-24;
var
  one                     : TCdouble;
  rj, xt, yt, zt, pt      : TCdouble;
  sum, a, b, rho, A0      : TCdouble;
  tau, rcx, lamda, Am     : TCdouble;
  sqrtx, sqrty, sqrtz, sqrtp, dm, em : TCdouble;
  delta                   : TCdouble;
  c1, c2, c3              : TCdouble;
  c4, c5, c6              : TCdouble;
  X0, Y0, Z0, P0          : TCdouble;
  E2, E3, E4, E5          : TCdouble;
  d0, d2, d3, d4, d5, d6  : TCdouble;
  p4                      : TCdouble;
  powa, def               : TCdouble;
  Q, pm                   : double;
  test, m                 : integer;
begin
  m := 0;
  if cabs(x) = 0 then inc(m);
  if cabs(y) = 0 then inc(m);
  if cabs(z) = 0 then inc(m);
  if cabs(p) = 0 then inc(m);
  if m > 1 then begin
    m := 0;
    result := MCdouble(0, 0);
    goto Ext;
  end;

  c1 := MCdouble(3 / 14, 0);
  c2 := MCdouble(1 / 6, 0);
  c3 := MCdouble(9 / 88, 0);
  c4 := MCdouble(3 / 22, 0);
  c5 := MCdouble(9 / 52, 0);
  c6 := MCdouble(3 / 26, 0);
  d0 := MCdouble(0, 0);
  d2 := MCdouble(2, 0);
  d3 := MCdouble(3, 0);
  d4 := MCdouble(4, 0);
  d5 := MCdouble(5, 0);
  d6 := MCdouble(6, 0);
  sum := MCdouble(0, 0);
  one := MCdouble(1, 0);
  if (p.r <= 0) and (y.r > 0) then test := -1
                              else test := 1;
  if test > 0 then begin
    xt := x;
    yt := y;
    zt := z;
    pt := p;
    a  := MCdouble(0, 0);
    b  := MCdouble(0, 0);
    rcx := MCdouble(0, 0);
  end
  else begin
    xt := minc3d(x, y, z);
    zt := maxc3d(x, y, z);
    yt := cadd(x, cadd(y, csub(z, cadd(xt, zt))));
    if cabs(csub(yt, p)) <> 0 then a := cdiv(one, csub(yt, p))  // 分母ゼロ回避　　{基本的には分母がゼロに成ることはないはずですがデバック用として入れてあります}
                              else a := MCdouble(+1E100, 0);
    b := cmul(cmul(a, csub(zt, yt)), csub(yt, xt));
    pt := cadd(yt,  b);
    rho := cmul(xt, cdiv(zt, yt));
    tau := cmul(p, cdiv(pt, yt));
    rcx := rcd(rho, tau);
  end;
  A0 := cdiv(cadd(xt, cadd(yt, cadd(zt, cadd(pt, pt)))), d5);
  AM := A0;
  delta := cmul(csub(pt, xt), cmul(csub(pt, yt), csub(pt, zt)));
  Q := power(r / 4, -1 / 6) * max(cabs(csub(A0, xt)), max(cabs(csub(A0, yt)),
                              max(cabs(csub(A0, zt)), cabs(csub(A0, pt)))));
  m := 0;
  repeat
    sqrtx := tsqrt(xt);                                  // Varcomplexsqrt
    sqrty := tsqrt(yt);                                  // Varcomplexsqrt
    sqrtz := tsqrt(zt);                                  // Varcomplexsqrt
    sqrtp := tsqrt(pt);                                  // Varcomplexsqrt
    lamda := cadd(cmul(sqrtx, cadd(sqrty, sqrtz)), cmul(sqrty, sqrtz));
    dm := cmul(cadd(sqrtp, sqrtx), cmul(cadd(sqrtp, sqrty), cadd(sqrtp,sqrtz)));
    p4 := tpower(d4, -3 * m);
    em := cdiv(cdiv(cmul(p4, delta), dm), dm);
    p4 := tpower(d4, -m);
    def := Rcd(one, cadd(one, em));
    sum := cadd(sum, cmul(cdiv(p4, dm), def));
    Am    := cdivd(cadd(Am, lamda), 4);
    xt    := cdivd(cadd(xt, lamda), 4);
    yt    := cdivd(cadd(yt, lamda), 4);
    zt    := cdivd(cadd(zt, lamda), 4);
    pt    := cdivd(cadd(pt, lamda), 4);
    m := m + 1;
  until power(4, -m) * Q < cabs(am);
  p4 := tpower(d4, m);
  X0 := cdiv(cdiv(csub(A0, x), p4), Am);
  Y0 := cdiv(cdiv(csub(A0, y), p4), Am);
  Z0 := cdiv(cdiv(csub(A0, z), p4), Am);
  P0 := cdivd(csub(csub(csub(d0, X0), Y0), Z0), 2);
  E2 := cadd(cadd(cmul(X0, Y0), cmul(X0, Z0)), cmul(Y0, Z0));
  E2 := csub(E2, cmul(cmul(d3, P0), P0));

  E3 := cmul(d4, cmul(P0, cmul(P0, P0)));
  E3 := cadd(cmul(X0, cmul(Y0, Z0)), cadd(cmul(d2, cmul(E2, P0)), E3));
  Pm := P0.r * P0.r + P0.i * P0.i;
  if Pm > 1e-100 then begin                                   // 分母ゼロ回避　　　　　　　{誤差の計算なので条件によって分母がゼロに成る事がありますが}
    E4 := cadd(cmul(E2, P0), cmul(d3, cmul(P0, cmul(P0, P0))));                            {ゼロに成る程誤差が小さい場合計算結果に影響しません}
    E4 := cadd(cmul(d2, cmul(X0, cmul(Y0, Z0))), E4);
    E4 := cdiv(E4, P0);
  end
  else
    E4 := MCdouble(0, 0);
  E5 := cmul(X0, cmul(Y0, cmul(Z0, cmul(P0, P0))));
  p4 := tpower(d4, -m);                                  // Varcomplexpower
  powa := tpower(Am, -3 / 2);　　　　　　　　　　　　　　{複素数のX^Yを使用します　複素数計算で1/sqrt(Am^3)を使用すると計算結果があわない事があります}
  def := csub(one, cmul(c1, E2));
  def := cadd(def, cmul(c2, E3));
  def := cadd(def, cmul(c3, cmul(E2, E2)));
  def := csub(def, cmul(c4, E4));
  def := csub(def, cmul(c5, cmul(E2, E3)));
  def := cadd(def, cmul(c6, E5));
  rj := cadd(cmul(p4, cmul(powa, def)), cmul(d6, sum));
  if test < 0 then
    rj := cmul(a, (cadd(cmul(b ,rj), cmul(d3, csub(rcx, rfd(xt, yt, zt))))));
  result := rj;
  form1.Canvas.TextOut(250,320,'             ');
  form1.Canvas.TextOut(250,320,'rj 判定 ' + floatTostr(test));

Ext:
  Form1.Memo1.Lines.Append('RJ Loop数 = ' + intTostr(m));
end;


var
  rcdt : array[0..5] of array[0..1] of TCdouble;
  rcan : array[0..5] of array[0..1] of double;

procedure datasetRc;
begin
  rcdt[0,0] := Vc( 0, 0);   rcdt[0, 1] := Vc(1/4, 0);
  rcdt[1,0] := Vc(9/4, 0);  rcdt[1, 1] := Vc(2, 0);
  rcdt[2,0] := Vc( 0, 0);   rcdt[2, 1] := Vc(0, 1);
  rcdt[3,0] := Vc( 0,-1);   rcdt[3, 1] := Vc(0, 1);
  rcdt[4,0] := Vc(1/4, 0);  rcdt[4, 1] := Vc(-2, 0);
  rcdt[5,0] := Vc( 0, 1);   rcdt[5, 1] := Vc(-1, 0);

  rcan[0,0] := 3.1415926535898;   rcan[0,1] := 0;
  rcan[1,0] := 0.69314718055995;  rcan[1,1] := 0;
  rcan[2,0] := 1.1107207345396;   rcan[2,1] := -1.1107207345396;
  rcan[3,0] := 1.2260849569072;   rcan[3,1] := -0.34471136988768;
  rcan[4,0] := 0.23104906018665;  rcan[4,1] := 0;
  rcan[5,0] := 0.77778596920447;  rcan[5,1] := 0.19832484993429;
end;

var
  rfdt : array[0..5] of array[0..2] of TCdouble;
  rfan : array[0..5] of array[0..1] of double;

procedure datasetRf;
begin
  rfdt[0,0] := Vc( 1, 0); rfdt[0,1] := Vc( 2, 0); rfdt[0,2] := Vc( 0, 0);
  rfdt[1,0] := Vc( 0, 1); rfdt[1,1] := Vc( 0,-1); rfdt[1,2] := Vc( 0, 0);
  rfdt[2,0] := Vc(-1, 1); rfdt[2,1] := Vc( 0, 1); rfdt[2,2] := Vc( 0, 0);
  rfdt[3,0] := Vc( 2, 0); rfdt[3,1] := Vc( 3, 0); rfdt[3,2] := Vc( 4, 0);
  rfdt[4,0] := Vc( 0, 1); rfdt[4,1] := Vc( 0,-1); rfdt[4,2] := Vc( 2, 0);
  rfdt[5,0] := Vc(-1, 1); rfdt[5,1] := Vc( 0, 1); rfdt[5,2] := Vc( 1,-1);

  rfan[0,0] := 1.3110287771461;  rfan[0,1] := 0;
  rfan[1,0] := 1.8540746773014;  rfan[1,1] := 1.8540746773014;
  rfan[2,0] := 0.79612586584234; rfan[2,1] := -1.2138566698365;
  rfan[3,0] := 0.58408284167715; rfan[3,1] := 0;
  rfan[4,0] := 1.0441445654064;  rfan[4,1] := 0;
  rfan[5,0] := 0.93912050218619; rfan[5,1] := -0.53296252018635;
end;

var
  rjdt : array[0..9] of array[0..3] of TCdouble;
  rjan : array[0..9] of array[0..1] of double;

procedure datasetRj;
begin
  rjdt[0,0] := Vc( 0, 0); rjdt[0,1] := Vc( 1, 0); rjdt[0,2] := Vc( 2, 0); rjdt[0,3] := Vc( 3, 0);
  rjdt[1,0] := Vc( 2, 0); rjdt[1,1] := Vc( 3, 0); rjdt[1,2] := Vc( 4, 0); rjdt[1,3] := Vc( 5, 0);
  rjdt[2,0] := Vc( 2, 0); rjdt[2,1] := Vc( 3, 0); rjdt[2,2] := Vc( 4, 0); rjdt[2,3] := Vc(-1, 1);
  rjdt[3,0] := Vc( 0, 1); rjdt[3,1] := Vc( 0,-1); rjdt[3,2] := Vc( 0, 0); rjdt[3,3] := Vc( 2, 0);
  rjdt[4,0] := Vc(-1, 1); rjdt[4,1] := Vc(-1,-1); rjdt[4,2] := Vc( 1, 0); rjdt[4,3] := Vc( 2, 0);
  rjdt[5,0] := Vc( 0, 1); rjdt[5,1] := Vc( 0,-1); rjdt[5,2] := Vc( 0, 0); rjdt[5,3] := Vc( 1,-1);
  rjdt[6,0] := Vc(-1, 1); rjdt[6,1] := Vc(-1,-1); rjdt[6,2] := Vc( 1, 0); rjdt[6,3] := Vc(-3, 1);
  rjdt[7,0] := Vc(-1, 1); rjdt[7,1] := Vc(-2,-1); rjdt[7,2] := Vc( 0,-1); rjdt[7,3] := Vc(-1, 1);
  rjdt[8,0] := Vc( 2, 0); rjdt[8,1] := Vc( 3, 0); rjdt[8,2] := Vc( 4, 0); rjdt[8,3] := Vc(-0.5, 0);
  rjdt[9,0] := Vc( 2, 0); rjdt[9,1] := Vc( 3, 0); rjdt[9,2] := Vc( 4, 0); rjdt[9,3] := Vc(-5, 0);

  rjan[0,0] :=  0.77688623778582;        rjan[0,1] :=  0;
  rjan[1,0] :=  0.14297579667157;        rjan[1,1] :=  0;
  rjan[2,0] :=  0.13613945827771;        rjan[2,1] := -0.38207561624427;
  rjan[3,0] :=  1.6490011662711;         rjan[3,1] :=  0;
  rjan[4,0] :=  0.94148358841220;        rjan[4,1] :=  0;
  rjan[5,0] :=  1.8260115229009;         rjan[5,1] :=  1.2290661908643;
  rjan[6,0] := -0.61127970812028;        rjan[6,1] := -1.0684038390007;
  rjan[7,0] :=  1.8249027393704;         rjan[7,1] := -1.2218475784827;
  rjan[8,0] :=  0.24723819703052;        rjan[8,1] :=  0;
  rjan[9,0] := -0.12711230042964;        rjan[9,1] :=  0;
end;

procedure TForm1.Rctest1Click(Sender: TObject);
var
  i : integer;
  x, y: TCdouble;
  ans0r, ans0i: double;
  ans       : TCdouble;
begin
  Form1.Memo1.clear;
  datasetRc;
  i := RcRadio.ItemIndex;
  x := rcdt[i,0]; y := rcdt[i,1];
  ans0r := rcan[i,0]; ans0i := rcan[i,1];
  Rcansr.Text := floatTostr(ans0r);
  Rcansi.Text := floatTostr(ans0i);
  ans := RCd(x, y);
  Rcdtxr.Text := floatTostr(x.r); Rcdtxi.Text := floatTostr(x.i);
  Rcdtyr.Text := floatTostr(y.r); Rcdtyi.Text := floatTostr(y.i);

  Rcclc0.Text := floatTostr(ans.r); Rcclc1.Text := floatTostr(ans.i);
end;

procedure TForm1.Rctest2Click(Sender: TObject);
var
  dinxr, dinxi: double;
  dinyr, dinyi: double;
  ch: integer;
  x, y: TCdouble;
  ans : TCdouble;
begin
  val(Rcdtxr.Text, dinxr, ch);
  if ch <> 0 then begin
    application.MessageBox('dtxrに間違いがあります。','注意',0);
    exit;
  end;
  val(Rcdtxi.Text, dinxi, ch);
  if ch <> 0 then begin
    application.MessageBox('dtxiに間違いがあります。','注意',0);
    exit;
  end;
  val(Rcdtyr.Text, dinyr, ch);
  if ch <> 0 then begin
    application.MessageBox('dtyrに間違いがあります。','注意',0);
    exit;
  end;
  val(Rcdtyi.Text, dinyi, ch);
  if ch <> 0 then begin
    application.MessageBox('dtyiに間違いがあります。','注意',0);
    exit;
  end;
  memo1.Clear;
  x := Vc( dinxr, dinxi);
  y := Vc( dinyr, dinyi);
  ans := RCd(x, y);
  memo1.Lines.Append(floatTostr(ans.r) + ' ' + floatTostr(ans.i) + 'i');
end;

procedure TForm1.Rftest1Click(Sender: TObject);
var
  i : integer;
  x, y, z: TCdouble;
  ans0r, ans0i: double;
  ans       : TCdouble;
begin
  Form1.Memo1.clear;
  datasetRf;
  i := RfRadio.ItemIndex;
  x := rfdt[i,0]; y := rfdt[i,1]; z := rfdt[i,2];
  ans0r := rfan[i,0]; ans0i := rfan[i,1];
  Rfansr.Text := floatTostr(ans0r);
  Rfansi.Text := floatTostr(ans0i);
  ans := RFd(x, y, z);
  Rfdtxr.Text := floatTostr(x.r); Rfdtxi.Text := floatTostr(x.i);
  Rfdtyr.Text := floatTostr(y.r); Rfdtyi.Text := floatTostr(y.i);
  Rfdtzr.Text := floatTostr(z.r); Rfdtzi.Text := floatTostr(z.i);

  Rfclc0.Text := floatTostr(ans.r); Rfclc1.Text := floatTostr(ans.i);
end;

procedure TForm1.Rftest2Click(Sender: TObject);
var
  dinxr, dinxi: double;
  dinyr, dinyi: double;
  dinzr, dinzi: double;
  ch: integer;
  x, y, z: TCdouble;
  ans : TCdouble;
begin
  val(Rfdtxr.Text, dinxr, ch);
  if ch <> 0 then begin
    application.MessageBox('dtxrに間違いがあります。','注意',0);
    exit;
  end;
  val(Rfdtxi.Text, dinxi, ch);
  if ch <> 0 then begin
    application.MessageBox('dtxiに間違いがあります。','注意',0);
    exit;
  end;
  val(Rfdtyr.Text, dinyr, ch);
  if ch <> 0 then begin
    application.MessageBox('dtyrに間違いがあります。','注意',0);
    exit;
  end;
  val(Rfdtyi.Text, dinyi, ch);
  if ch <> 0 then begin
    application.MessageBox('dtyiに間違いがあります。','注意',0);
    exit;
  end;
  val(Rfdtzr.Text, dinzr, ch);
  if ch <> 0 then begin
    application.MessageBox('dtzrに間違いがあります。','注意',0);
    exit;
  end;
  val(Rfdtzi.Text, dinzi, ch);
  if ch <> 0 then begin
    application.MessageBox('dtziに間違いがあります。','注意',0);
    exit;
  end;
  memo1.Clear;
  x := Vc( dinxr, dinxi);
  y := Vc( dinyr, dinyi);
  z := Vc( dinzr, dinzi);
  ans := Rfd(x, y, z);
  memo1.Lines.Append(floatTostr(ans.r) + ' ' + floatTostr(ans.i) + 'i');
end;

procedure TForm1.RJtest1Click(Sender: TObject);
var
  i : integer;
  x, y, z, p: TCdouble;
  ans0r, ans0i: double;
  ans       : TCdouble;
begin
  Form1.Memo1.clear;
  datasetRj;
  i := RJRadio.ItemIndex;
  x := rjdt[i,0]; y := rjdt[i,1]; z := rjdt[i,2]; p := rjdt[i, 3];
  ans0r := rjan[i,0]; ans0i := rjan[i,1];
  RJansr.Text := floatTostr(ans0r);
  RJansi.Text := floatTostr(ans0i);
  ans := RJd(x, y, z, p);
  RJdtxr.Text := floatTostr(x.r); RJdtxi.Text := floatTostr(x.i);
  RJdtyr.Text := floatTostr(y.r); RJdtyi.Text := floatTostr(y.i);
  RJdtzr.Text := floatTostr(z.r); RJdtzi.Text := floatTostr(z.i);
  RJdtpr.Text := floatTostr(p.r); RJdtpi.Text := floatTostr(p.i);

  RJclc0.Text := floatTostr(ans.r); RJclc1.Text := floatTostr(ans.i);
end;


procedure TForm1.Rjtest2Click(Sender: TObject);
var
  dinxr, dinxi: double;
  dinyr, dinyi: double;
  dinzr, dinzi: double;
  dinpr, dinpi: double;
  ch: integer;
  x, y, z, p : TCdouble;
  ans : TCdouble;
begin
  val(RJdtxr.Text, dinxr, ch);
  if ch <> 0 then begin
    application.MessageBox('dtxrに間違いがあります。','注意',0);
    exit;
  end;
  val(RJdtxi.Text, dinxi, ch);
  if ch <> 0 then begin
    application.MessageBox('dtxiに間違いがあります。','注意',0);
    exit;
  end;
  val(RJdtyr.Text, dinyr, ch);
  if ch <> 0 then begin
    application.MessageBox('dtyrに間違いがあります。','注意',0);
    exit;
  end;
  val(RJdtyi.Text, dinyi, ch);
  if ch <> 0 then begin
    application.MessageBox('dtyiに間違いがあります。','注意',0);
    exit;
  end;
  val(RJdtzr.Text, dinzr, ch);
  if ch <> 0 then begin
    application.MessageBox('dtzrに間違いがあります。','注意',0);
    exit;
  end;
  val(RJdtzi.Text, dinzi, ch);
  if ch <> 0 then begin
    application.MessageBox('dtziに間違いがあります。','注意',0);
    exit;
  end;
  val(RJdtpr.Text, dinpr, ch);
  if ch <> 0 then begin
    application.MessageBox('dtprに間違いがあります。','注意',0);
    exit;
  end;
  val(RJdtpi.Text, dinpi, ch);
  if ch <> 0 then begin
    application.MessageBox('dtpiに間違いがあります。','注意',0);
    exit;
  end;
  memo1.Clear;
  x := Vc( dinxr, dinxi);
  y := Vc( dinyr, dinyi);
  z := Vc( dinzr, dinzi);
  p := Vc( dinpr, dinpi);
  ans := RJd(x, y, z, p);
  memo1.Lines.Append(floatTostr(ans.r) + ' ' + floatTostr(ans.i) + 'i');
end;

end.

　RC_RF_RJ_checkCdouble.zip


各種プログラム計算例に戻る