透視変換
ここでの透視変換は、三次元のものを二次元に変換するのではなく、元々二次元の画像を三次元上で移動回転、せん断等を行い、二次元画面上に表示しています。
元のデーターには、奥行きはないことになります。
同じ様な変形を行うのなら、射影変換(ホモグラフィ)の方が扱い易いと思います。
透視変換の方法や考え方は、Webで検索すれば、沢山出てくるので、そちらを参照して下さい。
プログラムの作成に当たっては、画像処理入門(透視変換)を利用させていただきました。
入力項目と、画像の移動回転
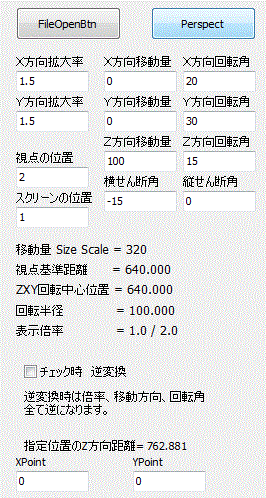
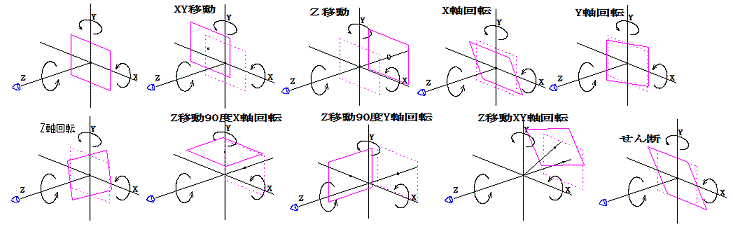
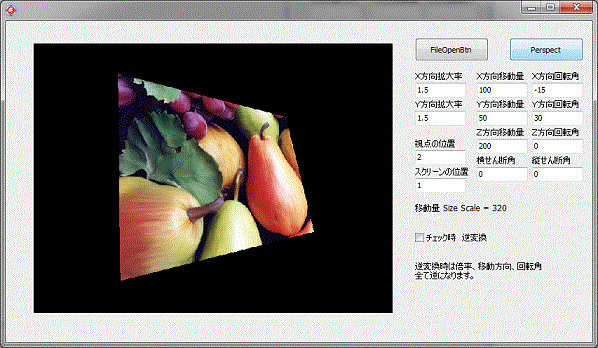
上図右は、各軸 X、Y、Zに対する元画像の移動を示しています。
視点(カメラ)は、Z軸上あり、XY軸上にある画像を見ることになります。
Webには、透視変換について色々な説明がなされたものがありますが、軸上にある画像をカメラで撮影し、投影機でスクリーン上に投影した画像を見ると考えたほうが、分かり易いと思います。
カメラで撮影した距離と、投影機からスクリーンまでの距離が等しければ、等倍になりスクリーンの距離が遠ければ大きく投影さり、近くなれば小さく投影されます。
スクリーンの位置は、単に投影される画像の大きさを変えるだけです。
視点の位置については、視点の距離が遠くなれば、小さく見えるようになり、画像が回転した時の台形に見える台形の底辺の長さと、上辺の長さの差が小さくなることになります。
移動、回転、せん断は、XYZ軸を基準に行いますが、移動方向 Z は分かりやすくするため、正の値でいれると、本来の軸座標とは反対に移動するように設定してあります、その為、正の値の場合、視点(カメラ)及び回転軸から、遠ざかる方向へ移動します。
Z軸の値を大きくすると、回転により、視点側に近づきますが、視点との距離がゼロになると、画像の一点だけが表示されることになり、更にZの値を大きくすると、画像が視点の後ろに行ってしまいます。その時は単純に画像が裏返しになるだけです。
画像を回転し、画像が視点との方向に完全に平行になると、画像には厚さがないため、表示されなくなります。
チェックボックスのチェック時逆変換は、逆行列で、入力座標と、出力座標を入れ替えていない為、透視変換した画像を元へ戻すことが出来ます。
逆変換なので、拡大、移動、回転等は、全て逆になります。
但し、変換時の入力値を記憶していないと、正しく元へ戻すのは容易ではありません。
回転、移動、逆行列は全て4x4のマトリックスを使用して行います、次のプログラム例を参照して下さい。
//***************************
// 透視変換(線形補間法)
//***************************
procedure TForm1.perspect;
var
i, j, m, n : Integer;
x, y, z, w : Double;
p, q : Double;
k : Karray;
xs, ys : Integer;
xsp, ysp : integer;
db, dg, dr : Integer;
xp, yp : double;
begin
if not inputcheck then exit; // 条件設定の確認と
xs := GWidth div 2; // X中心位置の計算
ys := GHeight div 2; // Y中心位置の計算
xsp := xs;
if Odd(GWidth) then xsp := xs + 1; // 画像幅サイズが奇数の時の補正左右対称になりません
ysp := ys;
if Odd(GHeight) then ysp := ys + 1; // 画像高さサイズが奇数の時の補正上下対象になりません
parametrs(k, ax, ay, px, py, pz, rz, rx, ry, v, s, tx, ty, xs, ys); // 変換パラメータk[]の決定
// 透視変換画像計算
for i := -ys to ysp - 1 do
for j := -xs to xsp - 1 do begin
// 元画像に対する座標計算
x := k[0] * j + k[1] * i + k[2];
y := k[3] * j + k[4] * i + k[5];
w := k[9] * j + k[10] * i + k[11];
db := 0; // 元画像の座標外の時の値 黒に設定
dg := 0;
dr := 0;
if (abs(w) > 1e-6) then begin // 分母の値が小さい場合は計算しない w の値がゼロになる条件もあります
x := x / w; // 座標 X
y := y / w; // 座標 Y
if x < -xs then x := -xs - 1; // floorエラー防止 絶対値が大きくなりすぎるとエラー
if x > xsp then x := xsp; // floorエラー防止 Integerの値をこえてしまう
if y < -ys then y := -ys - 1; // floorエラー防止
if y > ysp then y := ysp; // floorエラー防止
m := floor(y); // y負方向に整数化
n := floor(x); // x負方向に整数化
q := y - m; // y補間係数
p := x - n; // x補間係数
// 線形補間計算
// ysp - 1, xsp - 1 は 線形補間の為行列が1小さくなる為です
if (m >= -ys) and (m < ysp - 1) and (n >= -xs) and (n < xsp - 1) then begin
db := Trunc((1.0 - q) * ((1.0 - p) * BlueMat[m + ys,n + xs]
+ P * BlueMat[m + ys,n + 1 + xs])
+ q * ((1.0 - p) * BlueMat[m + 1 + ys,n + xs]
+ P * BlueMat[m + 1 + ys,n + 1 + xs]));
dg := Trunc((1.0 - q) * ((1.0 - p) * GlueMat[m + ys,n + xs]
+ P * GlueMat[m + ys,n + 1 + xs])
+ q * ((1.0 - p) * GlueMat[m + 1 + ys,n + xs]
+ P * GlueMat[m + 1 + ys,n + 1 + xs]));
dr := Trunc((1.0 - q) * ((1.0 - p) * RlueMat[m + ys,n + xs]
+ P * RlueMat[m + ys,n + 1 + xs])
+ q * ((1.0 - p) * RlueMat[m + 1 + ys,n + xs]
+ P * RlueMat[m + 1 + ys,n + 1 + xs]));
end;
end;
BOutMat[i + ys, j + xs] := db; // 配列に保存
GOutMat[i + ys, j + xs] := dg;
ROutMat[i + ys, j + xs] := dr;
end;
Val(XpointEdit.Text,Xp, i);
if i <> 0 then Xp := 0; // 入力ミスがあったら Xp := 0に設定
Val(YpointEdit.Text,Yp, i);
if i <> 0 then Yp := 0; // 入力ミスがあったら Yp := 0に設定
z := k[6] * Xp + k[7] * -Yp + k[8]; // YP は方向が逆なので-にします Z方向計算
w := k[9] * Xp + k[10] * -Yp + k[11]; // YP は方向が逆なので-にします
z := z / w; // Z方向計算z方向距離
if not checkbox1.Checked then
Label2.Caption:= '指定位置のZ方向距離= ' + floatTostrF(-z, ffFixed, 10, 3)
else
Label2.Caption:= 'スクリーンの距離 = ' + floatTostrF(z, ffFixed, 10, 3)
end;
//***********************************************
// 変換パラメーターの設定
//
// k[]: 変換パラメータ
// a: 拡大率(x方向)
// b: 拡大率(y方向)
// x0: 移動量(x方向)
// y0: 移動量(y方向)
// z0: 移動量(z方向)
// z: 回転角(z方向,度)
// x: 回転角(x方向,度)
// y: 回転角(y方向,度)
// t: 視点の位置(z方向)
// s: スクリーンの位置(z方向)
// tx: せん断X方向
// ty: せん断y方向
//***********************************************
procedure TForm1.parametrs(var k: Karray; a, b, x0, y0, z0, z, x, y, t, s, tx, ty: Double; xs, ys: Integer); // 変換パラメータ決定
const
c = 1; // z 方向拡大率
var
l, m, n : T4x4Mat;
u, v, w : double; // 回転角
tanX : Double; // 横方向せん断
tanY : Double; // 縦方向せん断
ts : Double; // 大きさ単位係数
id : Double; // 視点からの基準距離
Zc : Double; // 視点からの回転中心距離
Zr : Double; // Z方向半径
begin
u := DegToRad(x); // X軸回転角
v := DegToRad(y); // Y軸回転角
w := DegToRad(z); // Z軸回転角
tanX := tan(DegToRad(-tx)); // tan(X軸せん断角)
tanY := tan(DegToRad( ty)); // tan(Y軸せん断角)
ts := xs; // 縦横で大きい方の値を単位に設定
if ys > ts then ts := ys;
id := ts * t; // 視点からの基準距離計算
Zr := z0; // Z方向半径基準値計算
Zc := (ts+Zr) * t; // Z方向移動時回転中心基準値
// 各値表示
IDLabel.Caption := Idistance + floatTostrF(id, ffFixed, 10, 3); // 視点からの基準距離
ZCLabel.Caption := Zcenter + floatTostrF(Zc, ffFixed, 10, 3); // 回転中心位置
ZrLabel.Caption := Zradius + floatTostrF(Zr, ffFixed, 10, 3); // Z方向半径
DispLabel.Caption := dispb + floatTostrF(s, ffFixed, 10, 1) + ' / ' + floatTostrF(t, ffFixed, 10, 1); // 表示倍率
// 正規化マトリックス
l[0, 0] := 1 / ts; l[0, 1] := 0; l[0, 2] := 0; l[0, 3] := 0; // 1 / ts は単位設定
l[1, 0] := 0; l[1, 1] := -1 / ts; l[1, 2] := 0; l[1, 3] := 0; // -1 / ts は単位設定 -1はY軸反転 winはy軸が逆
l[2, 0] := 0; l[2, 1] := 0; l[2, 2] := 1 / ts; l[2, 3] := 0; // 此処の1 / ts効果ありません
l[3, 0] := 0; l[3, 1] := 0; l[3, 2] := 0; l[3, 3] := 1;
// 拡大縮小マトリックス a X 方向 b y方向 c z方向
m[0, 0] := a; m[0, 1] := 0; m[0, 2] := 0; m[0, 3] := 0; // X 方向変倍率 a
m[1, 0] := 0; m[1, 1] := b; m[1, 2] := 0; m[1, 3] := 0; // y 方向変倍率 b
m[2, 0] := 0; m[2, 1] := 0; m[2, 2] := c; m[2, 3] := 0; // z 方向変倍率 c=1
m[3, 0] := 0; m[3, 1] := 0; m[3, 2] := 0; m[3, 3] := 1;
matrix(l, m, n); // 正規化マトリックス * 拡大縮小マトリックス
// 移動マトリックス
l[0, 0] := 1; l[0, 1] := 0; l[0, 2] := 0; l[0, 3] := 0;
l[1, 0] := 0; l[1, 1] := 1; l[1, 2] := 0; l[1, 3] := 0;
l[2, 0] := 0; l[2, 1] := 0; l[2, 2] := 1; l[2, 3] := 0;
l[3, 0] := x0 / ts; l[3, 1] := y0 / ts; l[3, 2] := z0 / ts; l[3, 3] := 1; // tsで割って移動量を設定単位にします
matrix(n, l, m); // * 移動マトリックス
// X方向 Y 方向 せん断マトリックス
n[0, 0] := 1; n[0, 1] := tanY; n[0, 2] := 0; n[0, 3] := 0; // tanY Y方向せん断
n[1, 0] := tanX; n[1, 1] := 1; n[1, 2] := 0; n[1, 3] := 0; // tanX X方向せん断
n[2, 0] := 0; n[2, 1] := 0; n[2, 2] := 1; n[2, 3] := 0;
n[3, 0] := 0; n[3, 1] := 0; n[3, 2] := 0; n[3, 3] := 1;
matrix(m, n, l); // * X方向 Y 方向 せん断マトリックス
// Z軸回転マトリックス (XY移動)
m[0, 0] := cos(w); m[0, 1] := sin(w); m[0, 2] := 0; m[0, 3] := 0; // w Z軸回転角
m[1, 0] := -sin(w); m[1, 1] := cos(w); m[1, 2] := 0; m[1, 3] := 0;
m[2, 0] := 0; m[2, 1] := 0; m[2, 2] := 1; m[2, 3] := 0;
m[3, 0] := 0; m[3, 1] := 0; m[3, 2] := 0; m[3, 3] := 1;
matrix(l, m, n); // * z軸回転マトリックス
// X軸回転マトリックス (YZ移動)
l[0, 0] := 1; l[0, 1] := 0; l[0, 2] := 0; l[0, 3] := 0;
l[1, 0] := 0; l[1, 1] := cos(u); l[1, 2] := -sin(u); l[1, 3] := 0; // u X軸回転角 y軸反転してあるのでsin符号変更
l[2, 0] := 0; l[2, 1] := sin(u); l[2, 2] := cos(u); l[2, 3] := 0;
l[3, 0] := 0; l[3, 1] := 0; l[3, 2] := 0; l[3, 3] := 1;
matrix(n, l, m); // * x軸回転マトリックス
// Y軸回転マトリックス (XZ移動)
n[0, 0] := cos(V); n[0, 1] := 0; n[0, 2] := sin(v); n[0, 3] := 0; // v Y軸回転角
n[1, 0] := 0; n[1, 1] := 1; n[1, 2] := 0; n[1, 3] := 0;
n[2, 0] := -sin(v); n[2, 1] := 0; n[2, 2] := cos(v); n[2, 3] := 0;
n[3, 0] := 0; n[3, 1] := 0; n[3, 2] := 0; n[3, 3] := 1;
matrix(m, n, l); // * y軸回転マトリックス
// 視点座標マトリックス
m[0, 0] := 1; m[0, 1] := 0; m[0, 2] := 0; m[0, 3] := 0;
m[1, 0] := 0; m[1, 1] := 1; m[1, 2] := 0; m[1, 3] := 0;
m[2, 0] := 0; m[2, 1] := 0; m[2, 2] := 1; m[2, 3] := 0; // m[2, 2] := -1の時はX軸y軸回転方向反転 z軸反転
m[3, 0] := 0; m[3, 1] := 0; m[3, 2] := t; m[3, 3] := 1; // t視点の位置
matrix(l, m, n); // * 視点座標変換マトリックス
// 透視変換マトリックス
l[0, 0] := 1; l[0, 1] := 0; l[0, 2] := 0; l[0, 3] := 0;
l[1, 0] := 0; l[1, 1] := 1; l[1, 2] := 0; l[1, 3] := 0;
l[2, 0] := 0; l[2, 1] := 0; l[2, 2] := 1; l[2, 3] := 1 / s; // s スクリーンの位置
l[3, 0] := 0; l[3, 1] := 0; l[3, 2] := 0; l[3, 3] := 0;
matrix(n, l, m); // * 透視変換マトリックス
// 正規化マトリックス
n[0, 0] := ts; n[0, 1] := 0; n[0, 2] := 0; n[0, 3] := 0; // ts 単位設定値
n[1, 0] := 0; n[1, 1] := -ts; n[1, 2] := 0; n[1, 3] := 0;
n[2, 0] := 0; n[2, 1] := 0; n[2, 2] := ts; n[2, 3] := 0;
n[3, 0] := 0; n[3, 1] := 0; n[3, 2] := 0; n[3, 3] := 1;
matrix(m, n, l); // * 正規化マトリックス
// 逆行列を求めなければ、変換後の形状を元へ戻す変換になります。
if not checkbox1.Checked then begin
// Z 方向は作図に使用しないのでゼロに設定、対角は1
l[2,0] := 0; l[2,1] := 0; l[2,2] := 1; l[2,3] := 0;
l := mat4inverse(l); // 4x4逆行列の計算
end;
// Xの項
K[0] := l[0,0];
K[1] := l[1,0];
k[2] := l[3,0];
// Yの項
K[3] := l[0,1];
K[4] := l[1,1];
k[5] := l[3,1];
// Zの項
K[6] := l[0,2];
K[7] := l[1,2];
K[8] := l[3,2];
// Wの項
K[9] := l[0,3];
k[10] := l[1,3];
k[11] := l[3,3];
end;
//***** matrix *** マトリックス掛け算 **********
// a: 入力マトリックス1
// b: 入力マトリックス2
// c: 出力マトリックス
//********************************************
procedure TForm1.matrix(a, b: T4x4Mat; var c: T4x4Mat); // matrix マトリックス掛け算
var
i, j, k: integer;
p : double;
begin
for i := 0 to 3 do
for j := 0 to 3 do begin
p := 0;
for k := 0 to 3 do p := p + a[i, k] * b[k, j];
c[i, j] := p;
end;
end;


上記のプログラム例では、移動のマトリックスが、拡大縮小の後に入っているため、Z方向の移動が、回転軸からの移動となる為、Z方向に移動すると、XY方向に回転した時、半径Zを持って画像が回転します。
この時の表示の位置の補正は出来ません。
どの様な順番で変換マトリックスを行うかは、用途に応じて決めれば良いと思います。
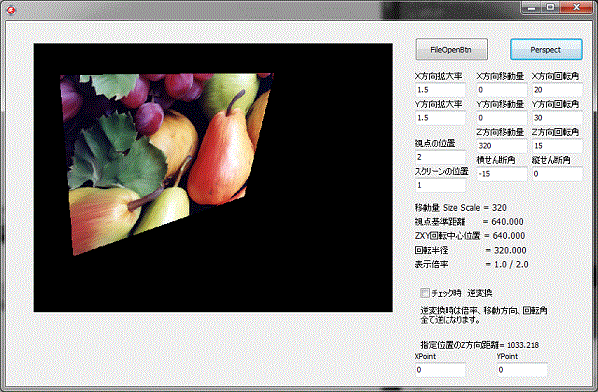
Z方向に移動320移動しているので、画像の中心位置が、回転により左上に移動しています。
回転角の方向によって、左右、上下に移動をします。
次の例は、移動マトリックスを、回転マトリックスの後にした場合の例です。
逆マトリックスは、4x4で行う必要はないので、3x3の逆マトリックスになっています。
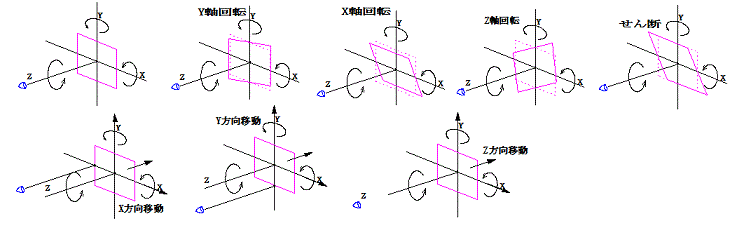
この場合の移動は、視点(カメラ)の位置に対する回転軸の移動になります。
Z方向の正移動は、回転軸そのものが、視点(カメラ)から遠ざかる方向へ移動します。
XY移動もそれぞれ、視点(カメラ)の位置に対する回転軸の移動となります。
//***************************
// 透視変換(線形補間法)
//***************************
procedure TForm1.perspect;
var
i, j, m, n : Integer;
x, y, w, p, q : Double;
k : Karray;
xs, ys : Integer;
xsp, ysp : integer;
db, dg, dr : Integer;
begin
if not inputcheck then exit; // 条件設定の確認と
xs := GWidth div 2; // X中心位置の計算
ys := GHeight div 2; // Y中心位置の計算
xsp := xs;
if Odd(GWidth) then xsp := xs + 1; // 画像幅サイズが奇数の時の補正左右対称になりません
ysp := ys;
if Odd(GHeight) then ysp := ys + 1; // 画像高さサイズが奇数の時の補正上下対象になりません
parametrs(k, ax, ay, px, py, pz, rz, rx, ry, v, s, tx, ty, xs, ys); // 変換パラメータk[]の決定
// 透視変換画像計算
for i := -ys to ysp - 1 do
for j := -xs to xsp - 1 do begin
// 元画像に対する座標計算
x := k[0] * j + k[1] * i + k[2];
y := k[3] * j + k[4] * i + k[5];
w := k[6] * j + k[7] * i + k[8];
db := 0; // 元画像の座標外の時の値 黒に設定
dg := 0;
dr := 0;
if (abs(w) > 1e-6) then begin // 分母の値が小さい場合は計算しない w の値がゼロになる条件もあります
x := x / w; // 座標 X
y := y / w; // 座標 Y
if x < -xs then x := -xs - 1; // floorエラー防止 絶対値が大きくなりすぎるとエラー
if x > xsp then x := xsp; // floorエラー防止 Integerの値をこえてしまう
if y < -ys then y := -ys - 1; // floorエラー防止
if y > ysp then y := ysp; // floorエラー防止
m := floor(y); // y負方向に整数化
n := floor(x); // x負方向に整数化
q := y - m; // y補間係数
p := x - n; // x補間係数
// 線形補間計算
// ysp - 1, xsp - 1 は 線形補間の為行列が1小さくなる為です
if (m >= -ys) and (m < ysp - 1) and (n >= -xs) and (n < xsp - 1) then begin
db := Trunc((1.0 - q) * ((1.0 - p) * BlueMat[m + ys,n + xs]
+ P * BlueMat[m + ys,n + 1 + xs])
+ q * ((1.0 - p) * BlueMat[m + 1 + ys,n + xs]
+ P * BlueMat[m + 1 + ys,n + 1 + xs]));
dg := Trunc((1.0 - q) * ((1.0 - p) * GlueMat[m + ys,n + xs]
+ P * GlueMat[m + ys,n + 1 + xs])
+ q * ((1.0 - p) * GlueMat[m + 1 + ys,n + xs]
+ P * GlueMat[m + 1 + ys,n + 1 + xs]));
dr := Trunc((1.0 - q) * ((1.0 - p) * RlueMat[m + ys,n + xs]
+ P * RlueMat[m + ys,n + 1 + xs])
+ q * ((1.0 - p) * RlueMat[m + 1 + ys,n + xs]
+ P * RlueMat[m + 1 + ys,n + 1 + xs]));
end;
end;
BOutMat[i + ys, j + xs] := db; // 配列に保存
GOutMat[i + ys, j + xs] := dg;
ROutMat[i + ys, j + xs] := dr;
end;
end;
//***********************************************
// 変換パラメーターの設定
//
// k[]: 変換パラメータ
// a: 拡大率(x方向)
// b: 拡大率(y方向)
// x0: 移動量(x方向)
// y0: 移動量(y方向)
// z0: 移動量(z方向)
// z: 回転角(z方向,度)
// x: 回転角(x方向,度)
// y: 回転角(y方向,度)
// t: 視点の位置(z方向)
// s: スクリーンの位置(z方向)
// tx: せん断X方向
// ty: せん断y方向
//***********************************************
procedure TForm1.parametrs(var k: Karray; a, b, x0, y0, z0, z, x, y, t, s, tx, ty: Double; xs, ys: Integer); // 変換パラメータ決定
const
c = 1; // z 方向拡大率
var
l, m, n : Dblarray;
aa: array[0..2] of array[0..2] of double;
u, v, w : double; // 回転角
tanX : Double; // 横方向せん断
tanY : Double; // 縦方向せん断
ts : Double; // 大きさ単位係数
begin
u := DegToRad(x); // X軸回転角
v := DegToRad(y); // Y軸回転角
w := DegToRad(z); // Z軸回転角
tanX := tan(DegToRad(-tx)); // tan(X軸せん断角)
tanY := tan(DegToRad( ty)); // tan(Y軸せん断角)
ts := xs; // 縦横で大きい方の値を単位に設定
if ys > ts then ts := ys;
// 正規化マトリックス
l[0, 0] := 1 / ts; l[0, 1] := 0; l[0, 2] := 0; l[0, 3] := 0; // 1 / ts は単位設定
l[1, 0] := 0; l[1, 1] := -1 / ts; l[1, 2] := 0; l[1, 3] := 0; // -1 / ts は単位設定 -1はY軸反転
l[2, 0] := 0; l[2, 1] := 0; l[2, 2] := 1; l[2, 3] := 0; // winはy軸が逆
l[3, 0] := 0; l[3, 1] := 0; l[3, 2] := 0; l[3, 3] := 1;
// 拡大縮小マトリックス a X 方向 b y方向 c z方向
m[0, 0] := a; m[0, 1] := 0; m[0, 2] := 0; m[0, 3] := 0; // X 方向変倍率 a
m[1, 0] := 0; m[1, 1] := b; m[1, 2] := 0; m[1, 3] := 0; // y 方向変倍率 b
m[2, 0] := 0; m[2, 1] := 0; m[2, 2] := c; m[2, 3] := 0; // z 方向変倍率 c=1
m[3, 0] := 0; m[3, 1] := 0; m[3, 2] := 0; m[3, 3] := 1;
matrix(l, m, n); // 正規化マトリックス * 拡大縮小マトリックス
// X方向 Y 方向 せん断マトリックス
l[0, 0] := 1; l[0, 1] := tanY; l[0, 2] := 0; l[0, 3] := 0; // tanY Y方向せん断
l[1, 0] := tanX; l[1, 1] := 1; l[1, 2] := 0; l[1, 3] := 0; // tanX X方向せん断
l[2, 0] := 0; l[2, 1] := 0; l[2, 2] := 1; l[2, 3] := 0;
l[3, 0] := 0; l[3, 1] := 0; l[3, 2] := 0; l[3, 3] := 1;
matrix(n, l, m); // * X方向 Y 方向 せん断マトリックス
// Z軸回転マトリックス (XY移動)
n[0, 0] := cos(w); n[0, 1] := sin(w); n[0, 2] := 0; n[0, 3] := 0; // w Z軸回転角
n[1, 0] := -sin(w); n[1, 1] := cos(w); n[1, 2] := 0; n[1, 3] := 0;
n[2, 0] := 0; n[2, 1] := 0; n[2, 2] := 1; n[2, 3] := 0;
n[3, 0] := 0; n[3, 1] := 0; n[3, 2] := 0; n[3, 3] := 1;
matrix(m, n, l); // * z軸回転マトリックス
// X軸回転マトリックス (YZ移動)
m[0, 0] := 1; m[0, 1] := 0; m[0, 2] := 0; m[0, 3] := 0;
m[1, 0] := 0; m[1, 1] := cos(u); m[1, 2] := -sin(u); m[1, 3] := 0; // u X軸回転角 y軸反転してあるのでsin符号変更
m[2, 0] := 0; m[2, 1] := sin(u); m[2, 2] := cos(u); m[2, 3] := 0;
m[3, 0] := 0; m[3, 1] := 0; m[3, 2] := 0; m[3, 3] := 1;
matrix(l, m, n); // * x軸回転マトリックス
// Y軸回転マトリックス (XZ移動)
l[0, 0] := cos(V); l[0, 1] := 0; l[0, 2] := sin(v); l[0, 3] := 0; // v Y軸回転角
l[1, 0] := 0; l[1, 1] := 1; l[1, 2] := 0; l[1, 3] := 0;
l[2, 0] := -sin(v); l[2, 1] := 0; l[2, 2] := cos(v); l[2, 3] := 0;
l[3, 0] := 0; l[3, 1] := 0; l[3, 2] := 0; l[3, 3] := 1;
matrix(n, l, m); // * y軸回転マトリックス
// 移動マトリックス
n[0, 0] := 1; n[0, 1] := 0; n[0, 2] := 0; n[0, 3] := 0;
n[1, 0] := 0; n[1, 1] := 1; n[1, 2] := 0; n[1, 3] := 0;
n[2, 0] := 0; n[2, 1] := 0; n[2, 2] := 1; n[2, 3] := 0;
n[3, 0] := x0 / ts; n[3, 1] := y0 / ts; n[3, 2] := z0 / ts; n[3, 3] := 1; // tsで割って移動量を設定単位にします
matrix(m, n, l); // * 移動マトリックス
// 視点座標マトリックス
m[0, 0] := 1; m[0, 1] := 0; m[0, 2] := 0; m[0, 3] := 0;
m[1, 0] := 0; m[1, 1] := 1; m[1, 2] := 0; m[1, 3] := 0;
m[2, 0] := 0; m[2, 1] := 0; m[2, 2] := 1; m[2, 3] := 0; // m[2, 2] := -1の時はX軸y軸回転方向反転 z軸反転
m[3, 0] := 0; m[3, 1] := 0; m[3, 2] := t; m[3, 3] := 1; // t視点の位置
matrix(l, m, n); // * 視点座標変換マトリックス
// 透視変換マトリックス
l[0, 0] := 1; l[0, 1] := 0; l[0, 2] := 0; l[0, 3] := 0;
l[1, 0] := 0; l[1, 1] := 1; l[1, 2] := 0; l[1, 3] := 0;
l[2, 0] := 0; l[2, 1] := 0; l[2, 2] := 1; l[2, 3] := 1 / s; // s スクリーンの位置
l[3, 0] := 0; l[3, 1] := 0; l[3, 2] := 0; l[3, 3] := 0;
matrix(n, l, m); // * 透視変換マトリックス
// 正規化マトリックス
n[0, 0] := ts; n[0, 1] := 0; n[0, 2] := 0; n[0, 3] := 0; // ts 単位設定値
n[1, 0] := 0; n[1, 1] := -ts; n[1, 2] := 0; n[1, 3] := 0;
n[2, 0] := 0; n[2, 1] := 0; n[2, 2] := 1; n[2, 3] := 0;
n[3, 0] := 0; n[3, 1] := 0; n[3, 2] := 0; n[3, 3] := 1;
matrix(m, n, l); // * 正規化マトリックス
// 3 * 3のマトリックスに変換 l[n, 2] l[2, n] を除外しています
aa[0, 0] := l[0, 0]; aa[0, 1] := l[0, 1]; aa[0, 2] := l[0, 3];
aa[1, 0] := l[1, 0]; aa[1, 1] := l[1, 1]; aa[1, 2] := l[1, 3];
aa[2, 0] := l[3, 0]; aa[2, 1] := l[3, 1]; aa[2, 2] := l[3, 3];
if checkbox1.Checked then begin
// 逆行列を求めなければ、変換後の形状を元へ戻す変換になります。
K[0] := aa[0,0];
K[1] := aa[1,0];
k[2] := aa[2,0];
K[3] := aa[0,1];
K[4] := aa[1,1];
k[5] := aa[2,1];
K[6] := aa[0,2];
K[7] := aa[1,2];
k[8] := aa[2,2];
end
else begin
// 3 * 3の逆マトリックス計算 detAの計算省略
// 座標計算時Xの項 及び Yの項を Wの項で割りますがその時、両方にdetAがあるので計算省略しています
// detAを計算しないのでゼロによる除算は発生しません
// detA := a[0,0] * a[1,1] * a[2,2] + a[1,0] * a[2,1] * a[0,2] + a[2,0] * a[0,1] * a[1,2]
// - a[0,0] * a[2,1] * a[1,2] - a[2,0] * a[1,1] * a[0,2] - a[1,0] * a[0,1] * a[2,2];
// xの項
K[0] := aa[1, 1] * aa[2, 2] - aa[1, 2] * aa[2, 1];
K[1] := aa[1, 2] * aa[2, 0] - aa[1, 0] * aa[2, 2];
K[2] := aa[1, 0] * aa[2, 1] - aa[1, 1] * aa[2, 0];
// yの項
K[3] := aa[0, 2] * aa[2, 1] - aa[0, 1] * aa[2, 2];
K[4] := aa[0, 0] * aa[2, 2] - aa[0, 2] * aa[2, 0];
K[5] := aa[0, 1] * aa[2, 0] - aa[0, 0] * aa[2, 1];
// wの項
K[6] := aa[0, 1] * aa[1, 2] - aa[0, 2] * aa[1, 1];
K[7] := aa[0, 2] * aa[1, 0] - aa[0, 0] * aa[1, 2];
K[8] := aa[0, 0] * aa[1, 1] - aa[0, 1] * aa[1, 0];
end;
end;
//***** matrix *** マトリックス掛け算 **********
// a: 入力マトリックス1
// b: 入力マトリックス2
// c: 出力マトリックス
//********************************************
procedure TForm1.matrix(a, b: Dblarray; var c: Dblarray); // matrix マトリックス掛け算
var
i, j, k: integer;
p : double;
begin
for i := 0 to 3 do
for j := 0 to 3 do begin
p := 0;
for k := 0 to 3 do p := p + a[i, k] * b[k, j];
c[i, j] := p;
end;
end;
Z方向の移動を200程行って回転をしていますが、画像の中心位置は移動しません。
又、X 及び Y移動により、回転後の画像を、表示枠の中心に移動することも可能です。
部分的に拡大する場合は、こちらの方が扱い易いかもしれません。
移動をマトリックスをどの位置で行うかは、使用目的によってでしょう。
場合によっては、回転前と回転後の両方にあっても良いかと思います。
こちらのプログラムには、保存モードはありません。
保存を追加する場合は、保存のあるプログラムもあるのでそちらを参照して下さい。
 persective.zip
persective.zip
画像処理一覧へ戻る
最初に戻る






