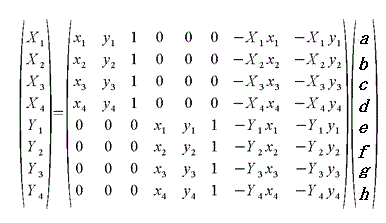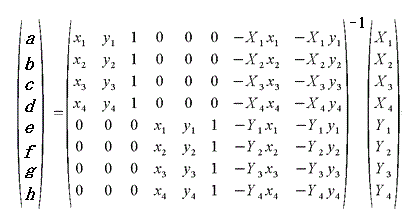射影変換(ホモグラフィ変換)
射影変換は、透視変換と同じ様に、画像を斜めに投影したかの様に変換しますが、画像の回転、視点、投影面の移動等はなく、単に画像の四隅四点の位置を指定することにより変換を行います。
逆変換を行えば、元の画像に戻すことが出来ます。

射影変換でもっとも有効な使い方は、斜めに写った写真の画像を、正面から見たように変換できることです。
上図例は、台形に変形した画像の四隅の座標を指定して、右側の画像のように正面から見た四角い画像に変換しています。
プログラムは、マウスで画像の四隅を指定しますが、正面から見た画像を台形画像に変換する場合は、画像の上で台形の形をマウスで入力します。
場所を指定してから、マウスで画像上をクリックします。
直接座標データーを編集しても構いません、此処でのサンプルプログラムでは、指定した座標のマークを画像上には表示していません。
プログラムの作成にあたって、射影変換の方法について、検索を行いましたが、なかなかこれというものが見つかりません。
とにかく、射影変換のソースを公開しているホームページのプログラムを作成してみることにしました。
しかし、殆どは、変換部分だけなのですが、前に作成したプログラムの変換部分だけを入れ替えることだけでテストしてみることが出来ました。
まずは最初に、"http://en.nicoptere.net/?p=59" HIDIHO!のHomographyにあったHomography.asをダウンロードして、Delphiのプログラムに変換をしてみました。
現在はなくなっているようです。
ここのホームページには、変換係数を求めるための元の連立方程式がないため、どの様にして計算式が求められたのかわかりません。
しかし、画像の高さ、幅を 1 (0<H<=1 0<W<=1) として、指定された座標の四点は0=<Px<Width, 0=<Py<Height として連立方程式を解いているようです。
変換の計算は非常に簡単な計算になってます。
座標の指定は、左上から、時計回りにしていします。
変換式は
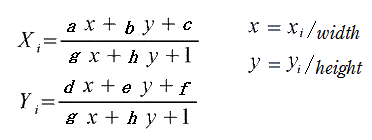 となっているようです。
となっているようです。
サンプルプログラムは此処でダウンロード出来る圧縮ファイルの中のホルダー名 HomographyM
の中にあります。
// 座標変換
function TForm1.Invert(u, v: Double; System: TSyst): TPoint;
var
Z : double;
begin
Z := system[6] * u + system[7] * v + 1;
if Z = 0 then Z := 1; // ゼロによる除算防止
Z := 1 / Z;
Result := Point(Trunc((system[0] * u + system[1] * v + system[2]) * Z),
Trunc((system[3] * u + system[4] * v + system[5]) * Z));
end;
// 変換パラメーターの設定
function TForm1.GetSystem(P: array of TPoint): TSyst;
var
System : TSyst;
sx, sy : Integer;
dx1, dx2 : Integer;
dy1, dy2 : Integer;
z, g, h : Double;
begin
sx := (P[0].x - P[1].x) + (P[2].x - P[3].x);
sy := (P[0].y - P[1].y) + (P[2].y - P[3].y);
dx1 := P[1].x - P[2].x;
dx2 := P[3].x - P[2].x;
dy1 := P[1].y - P[2].y;
dy2 := P[3].y - P[2].y;
z := (dx1 * dy2) - (dy1 * dx2);
if z = 0 then begin // ゼロだと無限大になるのでエラー
system[8] := 99; // system[8]はエラーフラグ 99 でエラー
Result := System;
exit;
end;
// 各係数の計算
g := ((sx * dy2) - (sy * dx2)) / z;
h := ((sy * dx1) - (sx * dy1)) / z;
system[0] := P[1].x - P[0].x + g * P[1].x;
system[1] := P[3].x - P[0].x + h * P[3].x;
system[2] := P[0].x;
system[3] := P[1].y - P[0].y + g * P[1].y;
system[4] := P[3].y - P[0].y + h * P[3].y;
system[5] := P[0].y;
system[6] := g;
system[7] := h;
system[8] := 0; // エラー無し
Result := System;
end;
// ホモグラフィ変換
procedure TForm1.Homography;
var
P : array[0..3] of TPoint;
System : TSyst;
i, J : Integer;
Pt : TPoint;
messtr : string;
begin
for i := 0 to 3 do begin
val(StringGrid1.Cells[1, i + 1], P[i].X, J);
if J <> 0 then begin
messtr := IntTostr(i + 1) + '番目のXの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
val(StringGrid1.Cells[2, i + 1], P[i].Y, J);
if J <> 0 then begin
messtr := IntTostr(i + 1) + '番目のYの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
end;
System := GetSystem(P); // 変換係数の取得
if System[8] = 99 then begin
application.MessageBox('座標入力値に誤りがあります。','注意',0);
exit;
end;
for i := 0 to Gheight - 1 do
for j := 0 to GWidth - 1 do begin
Pt := invert(j / GWidth, i / GHeight, system);
OutputBitmap.Canvas.Pixels[j, i] := InputDBitmap.Canvas.Pixels[Pt.x, Pt.y];
end;
end;
このプログラムで変換をすると、射影変換されているものを、長方形の画像に変換するようになっています。
長方形画像を四点で指定された形状に変換出来ないと最初は思いましたが、プログラムを良く眺めてみると、方程式に行列式を使用しているように思えるので、少し変更をして、逆行列の計算を追加してみました。
まず座標変換をする時に、指定座標を画像の幅と、画像の高さで除算してから、変換の計算をしていますが、この計算を、先に変換係数の中で計算をしてしまうことにします。
そうする事で、変換先の座標と、変換元の座標を直接変換出来る様になります。
その上で、逆行列の計算を追加します。
変換式は
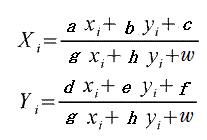 となります。
となります。
w の値は通常時は1で、逆行列で入力と出力を入れ替えた場合は、逆行列の値となります。
サンプルプログラムは此処でダウンロード出来る圧縮ファイルの中のホルダー名 Homography の中にあります。
// 座標変換
function TForm1.Invert(u, v: Double; System: TSyst): TPoint;
var
Z : double;
begin
Z := system[6] * u + system[7] * v + system[8];
if Z = 0 then Z := 1; // ゼロによる除算防止
Z := 1 / Z;
Result := Point(Trunc((system[0] * u + system[1] * v + system[2]) * Z),
Trunc((system[3] * u + system[4] * v + system[5]) * Z));
end;
// 変換パラメーターの設定
function TForm1.GetSystem(P: array of TPoint): TSyst;
var
System : TSyst;
sx, sy : Integer;
dx1, dx2 : Integer;
dy1, dy2 : Integer;
z, g, h : Double;
begin
sx := (P[0].x - P[1].x) + (P[2].x - P[3].x);
sy := (P[0].y - P[1].y) + (P[2].y - P[3].y);
dx1 := P[1].x - P[2].x;
dx2 := P[3].x - P[2].x;
dy1 := P[1].y - P[2].y;
dy2 := P[3].y - P[2].y;
z := (dx1 * dy2) - (dy1 * dx2);
if z = 0 then begin // ゼロだと無限大になるのでエラー
system[8] := 99; // system[8]はエラーフラグ 99 でエラー
Result := System;
exit;
end;
// 各係数の計算
g := ((sx * dy2) - (sy * dx2)) / z;
h := ((sy * dx1) - (sx * dy1)) / z;
system[0] := P[1].x - P[0].x + g * P[1].x; // a
system[1] := P[3].x - P[0].x + h * P[3].x; // b
system[2] := P[0].x; // c
system[3] := P[1].y - P[0].y + g * P[1].y; // d
system[4] := P[3].y - P[0].y + h * P[3].y; // e
system[5] := P[0].y; // f
system[6] := g;
system[7] := h;
system[8] := 1; // エラー無し 1が行列の正規の値
system[0] := system[0] / GWidth; // a
system[3] := system[3] / GWidth; // d
system[6] := system[6] / GWidth; // g
system[1] := system[1] / GHeight; // b
system[4] := system[4] / GHeight; // e
system[7] := system[7] / GHeight; // h
Result := System;
end;
// ホモグラフィ変換
procedure TForm1.Homography;
var
P : array[0..3] of TPoint;
System : TSyst;
i, J : Integer;
Pt : TPoint;
messtr : string;
a : T3x3mat;
begin
for i := 0 to 3 do begin
val(StringGrid1.Cells[1, i + 1], P[i].X, J);
if J <> 0 then begin
messtr := IntTostr(i + 1) + '番目のXの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
val(StringGrid1.Cells[2, i + 1], P[i].Y, J);
if J <> 0 then begin
messtr := IntTostr(i + 1) + '番目のYの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
end;
System := GetSystem(P); // 変換係数の取得
if System[8] = 99 then begin
application.MessageBox('座標入力値に誤りがあります。','注意',0);
exit;
end;
// 射影変換か逆変換かの選択です
if not CheckBox1.Checked then begin
// 逆行列の計算 座標変換時 分母と分子に detAが入るので detAの計算省略
a[0,0] := System[0];
a[1,0] := System[1];
a[2,0] := System[2];
a[0,1] := System[3];
a[1,1] := System[4];
a[2,1] := System[5];
a[0,2] := System[6];
a[1,2] := System[7];
a[2,2] := System[8];
// xの項
System[0] := a[1, 1] * a[2, 2] - a[1, 2] * a[2, 1];
System[1] := a[1, 2] * a[2, 0] - a[1, 0] * a[2, 2];
System[2] := a[1, 0] * a[2, 1] - a[1, 1] * a[2, 0];
// yの項
System[3] := a[0, 2] * a[2, 1] - a[0, 1] * a[2, 2];
System[4] := a[0, 0] * a[2, 2] - a[0, 2] * a[2, 0];
System[5] := a[0, 1] * a[2, 0] - a[0, 0] * a[2, 1];
// wの項
System[6] := a[0, 1] * a[1, 2] - a[0, 2] * a[1, 1];
System[7] := a[0, 2] * a[1, 0] - a[0, 0] * a[1, 2];
System[8] := a[0, 0] * a[1, 1] - a[0, 1] * a[1, 0];
end;
// 変換の実行
for i := 0 to Gheight - 1 do
for j := 0 to GWidth - 1 do begin
Pt := invert(j, i, system);
OutputBitmap.Canvas.Pixels[j, i] := InputDBitmap.Canvas.Pixels[Pt.x, Pt.y];
end;
end;
逆行列のdetAの計算値は、変換計算時の分母と分子の両方に入るので、計算を省略しています。
これで、長方形から、指定した四点を頂点とする画像へ、指定された四点の頂点座標から、長方形の画像へと両方の変換が可能となります。
更に、検索を重ねた結果、同じような計算をしている長方形を任意の四角形に変換する行列を見つけたので、Delphiのプログラムに組み込んでみました。
実際のプログラムソースの内容と、行列式の結果が若干違うようですので、ソースをダウンロードして、Delphiに移植してみました。
次の説明は、そのホームページあった解説をコピーしてプログラムにあわせて修正したものです。
0≦x≦W, 0≦y≦Hの領域にある長方形を0≦x≦1,
0≦y≦1の正方形に移す射影行列は自明(diag(1/W,1/H,1))なので、(0,0),(1,0),(0,1),(1,1)の4点を(Px,Py),(Qx,Qy),(Rx,Ry),(Sx,Sy)に移す射影変換を考える。
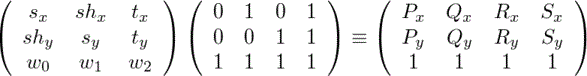
(≡は列ベクトルが斉次座標(homogeneous coordinate)として等価であることを表す)を満たすsx〜w2があるかどうかを考える。
上の合同式を展開。
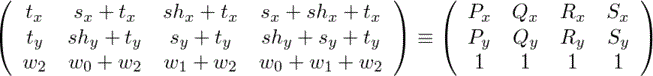
射影変換の斉次座標の定義より、(x y w)T≡(x/w y/w 1)Tなので、上の合同式は
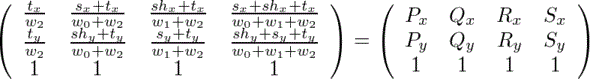
という等式にできる。つまり、
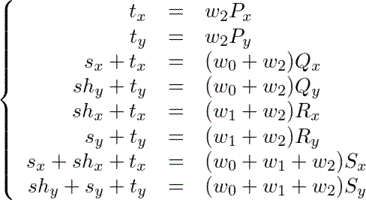
という連立方程式であり、これを解く(力づくで解くなら、tx,tyの次にw0,w1をまとめて求めると良い。)(一見複雑だが、分母は全て同じ)
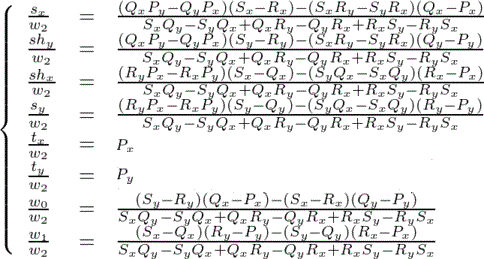
上記式と、次の行列式とでは、違う部分があります。
次の行列式は、プログラムから逆変換したものです。
計算は正しく出来てているので、連立方程式を解く過程で差異があると思われますが、検証をするのは大変なので省略します。
従って、w2=SxQy-SyQx+QxRy-QyRx+RxSy-RySxとすると、(0,0),(W,0),(0,H),(W,H)の4点を(Px,Py),(Qx,Qy),(Rx,Ry),(Sx,Sy)に移す射影変換は、
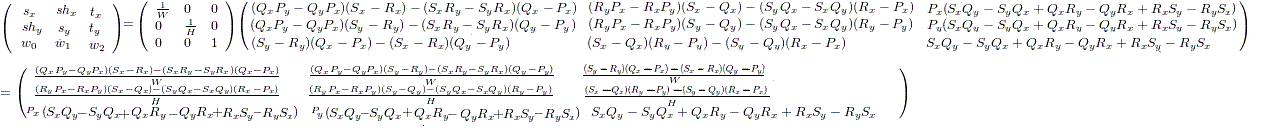
となります。
座標の変換式は
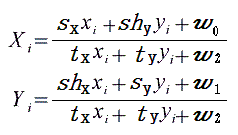
xi,yi に転送元の座標を入れて、転送先の座標を計算し値を書き込むと、書き込まれない座標が発生します。
xi,yi に転送先の座標を入れて、転送元の座標を計算し値を取得すると、任意の四点の形状から長方形に戻す計算となりますが、書き込まれない点は発生しません。
長方形から、任意の形状に正しく変換するためには、逆行列を使用して、転送元と転送先を入れ替える必要があります。
基本的に結果は前のプログラムと、同じ様になりました。
サンプルプログラムは此処でダウンロード出来る圧縮ファイルの中のホルダー名 HomographyR の中にあります。
// 座標変換
// 他のプログラムとは行と列が逆です
function TForm1.Invert(u, v: Double; System: TSyst): TPoint;
var
Z : double;
begin
Z := system[2] * u + system[5] * v + system[8];
if Z = 0 then Z := 1; // ゼロによる除算防止
Z := 1 / Z;
Result := Point(Trunc(((system[0] * u + system[3] * v + system[6]) * Z)),
Trunc(((system[1] * u + system[4] * v + system[7]) * Z)));
end;
// 変換パラメーターの設定
function TForm1.GetSystem(P: array of TPoint): TSyst;
var
System : TSyst;
Px,Qx,Rx,Sx : double;
Py,Qy,Ry,Sy : double;
begin
Px := P[0].X;
Qx := P[1].X;
Sx := P[2].X; // 指定の順番が違うのでここで変更しています
Rx := P[3].X;
Py := P[0].Y;
Qy := P[1].Y;
Sy := P[2].Y; // 指定の順番が違うのでここで変更しています
Ry := P[3].Y;
System[0] := (Qx*Py - Qy*Px)*(Sx - Rx) - (Sx*Ry - Sy*Rx)*(Qx - Px);
System[1] := (Qx*Py - Qy*Px)*(Sy - Ry) - (Sx*Ry - Sy*Rx)*(Qy - Py);
System[2] := (Sy - Ry)*(Qx - Px) - (Sx - Rx)*(Qy - Py);
System[3] := (Ry*Px - Rx*Py)*(Sx - Qx) - (Sy*Qx - Sx*Qy)*(Rx - Px);
System[4] := (Ry*Px - Rx*Py)*(Sy - Qy) - (Sy*Qx - Sx*Qy)*(Ry - Py);
System[5] := (Sx - Qx)*(Ry - Py) - (Sy - Qy)*(Rx - Px);
System[8] := Sx*Qy - Sy*Qx + Qx*Ry - Qy*Rx + Rx*Sy - Ry*Sx;
System[6] := Px * System[8];
System[7] := Py * System[8];
System[0] := System[0] / GWidth;
System[1] := System[1] / GWidth;
System[2] := System[2] / GWidth;
System[3] := System[3] / GHeight;
System[4] := System[4] / GHeight;
System[5] := System[5] / GHeight;
Result := System;
end;
// ホモグラフィ変換
procedure TForm1.Homography;
var
P : array[0..3] of TPoint;
System : TSyst;
i, J : Integer;
Pt : TPoint;
messtr : string;
a : T3x3mat;
begin
for i := 0 to 3 do begin
val(StringGrid1.Cells[1, i + 1], P[i].X, J);
if J <> 0 then begin
messtr := IntTostr(i + 1) + '番目のXの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
val(StringGrid1.Cells[2, i + 1], P[i].Y, J);
if J <> 0 then begin
messtr := IntTostr(i + 1) + '番目のYの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
end;
System := GetSystem(P); // 変換係数の取得
// 射影変換か逆変換かの選択です
if not CheckBox1.Checked then begin
// 逆行列の計算 座標変換時 分母と分子に detAが入るので detAの計算省略
a[0,0] := System[0];
a[1,0] := System[1];
a[2,0] := System[2];
a[0,1] := System[3];
a[1,1] := System[4];
a[2,1] := System[5];
a[0,2] := System[6];
a[1,2] := System[7];
a[2,2] := System[8];
// xの項
System[0] := a[1, 1] * a[2, 2] - a[1, 2] * a[2, 1];
System[1] := a[1, 2] * a[2, 0] - a[1, 0] * a[2, 2];
System[2] := a[1, 0] * a[2, 1] - a[1, 1] * a[2, 0];
// yの項
System[3] := a[0, 2] * a[2, 1] - a[0, 1] * a[2, 2];
System[4] := a[0, 0] * a[2, 2] - a[0, 2] * a[2, 0];
System[5] := a[0, 1] * a[2, 0] - a[0, 0] * a[2, 1];
// wの項
System[6] := a[0, 1] * a[1, 2] - a[0, 2] * a[1, 1];
System[7] := a[0, 2] * a[1, 0] - a[0, 0] * a[1, 2];
System[8] := a[0, 0] * a[1, 1] - a[0, 1] * a[1, 0];
end;
// 変換の実行
for i := 0 to Gheight - 1 do
for j := 0 to GWidth - 1 do begin
Pt := invert(j, i, system);
OutputBitmap.Canvas.Pixels[j, i] := InputDBitmap.Canvas.Pixels[Pt.x, Pt.y];
end;
end;
しかし、今までの変換では、指定した四点の頂点から、指定した四点への直接変換は出来ません。
あくまでも片方は、長方形の画像となります。
(一旦指定した四点から長方形に変換し、更に長方形から指定した四点の形状に変換すれば、変換が出来ないわけではありません。)
そこで、次は指定した四点の頂点から、指定した四点への変換を検討します。
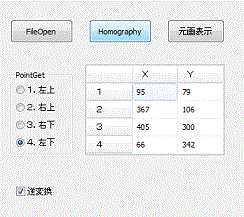
四点頂点指定から四点頂点指定変換
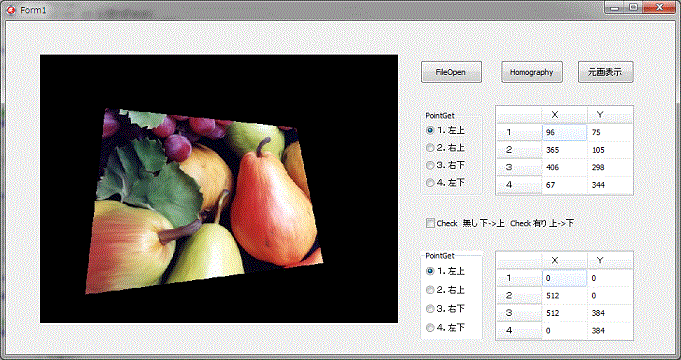
入力と出力画像の頂点四点を指定するため、座標入力グリッドを二つ用意してあります。
場所をラジオボタンで選択すれば画像上でマウスで指定が出来ます。
指定された場所のマーカーは表示されません。
こちらのプログラムの変換は、射影変換(ホモグラフィ)について理解してみる を参照して作成しました。
8次元連立方程式を8X8行列計算で解きますが、此処では4X4行列と2x2行列で求めています。
その方法は、遠近法の射影変換パラメータ計算の高速化にあるのでそれを参考にプログラムが組まれています。
サンプルプログラムは此処でダウンロード出来る圧縮ファイルの中のホルダー名 HomographyN、HomographyO の中にあります。
NとOの違いは、4×4の逆マトリックスにあり、Nは、マトリックス計算のアルゴリズムを最適化し高速に計算出来る様にしたもので、Oは通常の計算方法です。
// 4x4 逆行列
function mat4inverse(a: T4x4Mat): T4x4Mat;
var
dest : T4x4Mat;
b00, b01, b02, b03 : Double;
b04, b05, b06, b07 : Double;
b08, b09, b10, b11 : Double;
invDet : Double;
begin
// Cache the matrix values (makes for huge speed increases!)
b00 := a[0,0] * a[1,1] - a[0,1] * a[1,0];
b01 := a[0,0] * a[1,2] - a[0,2] * a[1,0];
b02 := a[0,0] * a[1,3] - a[0,3] * a[1,0];
b03 := a[0,1] * a[1,2] - a[0,2] * a[1,1];
b04 := a[0,1] * a[1,3] - a[0,3] * a[1,1];
b05 := a[0,2] * a[1,3] - a[0,3] * a[1,2];
b06 := a[2,0] * a[3,1] - a[2,1] * a[3,0];
b07 := a[2,0] * a[3,2] - a[2,2] * a[3,0];
b08 := a[2,0] * a[3,3] - a[2,3] * a[3,0];
b09 := a[2,1] * a[3,2] - a[2,2] * a[3,1];
b10 := a[2,1] * a[3,3] - a[2,3] * a[3,1];
b11 := a[2,2] * a[3,3] - a[2,3] * a[3,2];
// Calculate the determinant (inlined to avoid double-caching)
invDet := (b00 * b11 - b01 * b10 + b02 * b09 + b03 * b08 - b04 * b07 + b05 * b06);
if invDet = 0 then invDet := 1; // ゼロで除算するのを防止 プログラムにミスがなければゼロになりません
invDet := 1 / invDet;
dest[0,0] := ( a[1,1] * b11 - a[1,2] * b10 + a[1,3] * b09) * invDet;
dest[0,1] := (-a[0,1] * b11 + a[0,2] * b10 - a[0,3] * b09) * invDet;
dest[0,2] := ( a[3,1] * b05 - a[3,2] * b04 + a[3,3] * b03) * invDet;
dest[0,3] := (-a[2,1] * b05 + a[2,2] * b04 - a[2,3] * b03) * invDet;
dest[1,0] := (-a[1,0] * b11 + a[1,2] * b08 - a[1,3] * b07) * invDet;
dest[1,1] := ( a[0,0] * b11 - a[0,2] * b08 + a[0,3] * b07) * invDet;
dest[1,2] := (-a[3,0] * b05 + a[3,2] * b02 - a[3,3] * b01) * invDet;
dest[1,3] := ( a[2,0] * b05 - a[2,2] * b02 + a[2,3] * b01) * invDet;
dest[2,0] := ( a[1,0] * b10 - a[1,1] * b08 + a[1,3] * b06) * invDet;
dest[2,1] := (-a[0,0] * b10 + a[0,1] * b08 - a[0,3] * b06) * invDet;
dest[2,2] := ( a[3,0] * b04 - a[3,1] * b02 + a[3,3] * b00) * invDet;
dest[2,3] := (-a[2,0] * b04 + a[2,1] * b02 - a[2,3] * b00) * invDet;
dest[3,0] := (-a[1,0] * b09 + a[1,1] * b07 - a[1,2] * b06) * invDet;
dest[3,1] := ( a[0,0] * b09 - a[0,1] * b07 + a[0,2] * b06) * invDet;
dest[3,2] := (-a[3,0] * b03 + a[3,1] * b01 - a[3,2] * b00) * invDet;
dest[3,3] := ( a[2,0] * b03 - a[2,1] * b01 + a[2,2] * b00) * invDet;
Result := dest;
end;
// 変換パラメーター設定
function TForm1.getParam(sorc, dest: TpMat): T8mat;
var
Xl1, Xl2, Xl3, Xl4: Double;
xs1, xs2, xs3, xs4: Double;
Yl1, Yl2, Yl3, Yl4: Double;
ys1, ys2, ys3, ys4: Double;
tx, ty : T4x4Mat;
kc1, kc2, kc3, kc4: Double;
kx1, kx2, kx3, kx4: Double;
ky1, ky2, ky3, ky4: Double;
kf1, kf2, kf3, kf4: Double;
det_1 : Double;
Param : T8Mat;
C, F : Double;
I, J : integer;
begin
// 座標に 0 があると逆行列のdetが 0 になる事があるので僅かにずらします
for I := 0 to 3 do
for J := 0 to 1 do begin
if dest[I, J] = 0 then dest[I, J] := 0.2;
if sorc[I, J] = 0 then sorc[I, J] := 0.2;
end;
XL1 := dest[0, 0]; XL2 := dest[1, 0]; XL3 := dest[2, 0]; XL4 := dest[3, 0];
YL1 := dest[0, 1]; YL2 := dest[1, 1]; YL3 := dest[2, 1]; YL4 := dest[3, 1];
xs1 := sorc[0, 0]; xs2 := sorc[1, 0]; xs3 := sorc[2, 0]; xs4 := sorc[3, 0];
ys1 := sorc[0, 1]; ys2 := sorc[1, 1]; ys3 := sorc[2, 1]; ys4 := sorc[3, 1];
// X point
tx[0,0] := Xl1; tx[0,1] := Yl1; tx[0,2] := -Xl1 * xs1; tx[0,3] := -Yl1 * xs1;
tx[1,0] := Xl2; tx[1,1] := Yl2; tx[1,2] := -Xl2 * xs2; tx[1,3] := -Yl2 * xs2;
tx[2,0] := Xl3; tx[2,1] := Yl3; tx[2,2] := -Xl3 * xs3; tx[2,3] := -Yl3 * xs3;
tx[3,0] := Xl4; tx[3,1] := Yl4; tx[3,2] := -Xl4 * xs4; tx[3,3] := -Yl4 * xs4;
tx := mat4inverse(tx);
kx1 := tx[0,0] * xs1 + tx[0,1] * xs2 + tx[0,2] * xs3 + tx[0,3] * xs4;
kx2 := tx[1,0] * xs1 + tx[1,1] * xs2 + tx[1,2] * xs3 + tx[1,3] * xs4;
kx3 := tx[2,0] * xs1 + tx[2,1] * xs2 + tx[2,2] * xs3 + tx[2,3] * xs4;
kx4 := tx[3,0] * xs1 + tx[3,1] * xs2 + tx[3,2] * xs3 + tx[3,3] * xs4;
kc1 := tx[0,0] + tx[0,1] + tx[0,2] + tx[0,3];
kc2 := tx[1,0] + tx[1,1] + tx[1,2] + tx[1,3];
kc3 := tx[2,0] + tx[2,1] + tx[2,2] + tx[2,3];
kc4 := tx[3,0] + tx[3,1] + tx[3,2] + tx[3,3];
// Y point
ty[0,0] := Xl1; ty[0,1] := Yl1; ty[0,2] := -Xl1 * ys1; ty[0,3] := -Yl1 * ys1;
ty[1,0] := Xl2; ty[1,1] := Yl2; ty[1,2] := -Xl2 * ys2; ty[1,3] := -Yl2 * ys2;
ty[2,0] := Xl3; ty[2,1] := Yl3; ty[2,2] := -Xl3 * ys3; ty[2,3] := -Yl3 * ys3;
ty[3,0] := Xl4; ty[3,1] := Yl4; ty[3,2] := -Xl4 * ys4; ty[3,3] := -Yl4 * ys4;
ty := mat4inverse(ty);
ky1 := ty[0,0] * ys1 + ty[0,1] * ys2 + ty[0,2] * ys3 + ty[0,3] * ys4;
ky2 := ty[1,0] * ys1 + ty[1,1] * ys2 + ty[1,2] * ys3 + ty[1,3] * ys4;
ky3 := ty[2,0] * ys1 + ty[2,1] * ys2 + ty[2,2] * ys3 + ty[2,3] * ys4;
ky4 := ty[3,0] * ys1 + ty[3,1] * ys2 + ty[3,2] * ys3 + ty[3,3] * ys4;
kf1 := ty[0,0] + ty[0,1] + ty[0,2] + ty[0,3];
kf2 := ty[1,0] + ty[1,1] + ty[1,2] + ty[1,3];
kf3 := ty[2,0] + ty[2,1] + ty[2,2] + ty[2,3];
kf4 := ty[3,0] + ty[3,1] + ty[3,2] + ty[3,3];
det_1 := (kf3 * kc4) - (kc3 * kf4);
if det_1 = 0 then det_1 := 1; // 割り算エラー防止 プログラムにミスがなければゼロになりません
det_1 := 1 / det_1;
C := (kf3 * (kx4 - ky4) - kf4 * (kx3 - ky3)) * det_1;
F := (kc3 * (kx4 - ky4) - kc4 * (kx3 - ky3)) * det_1;
param[0] := kx1 - C * kc1;
param[1] := kx2 - C * kc2;
param[2] := C;
param[3] := ky1 - F * kf1;
param[4] := ky2 - F * kf2;
param[5] := F;
param[6] := kx3 - C * kc3;
param[7] := kx4 - C * kc4;
// param[6] := ky3 - F * kf3;
// param[7] := ky4 - F * kf4;
result := param;
end;
// 変換画像作成
procedure TForm1.draw(param: T9Mat);
var
i, j : Integer;
tmp : double;
tmpX, tmpY: Double;
X, Y : Integer;
begin
for i := 0 to Gheight - 1 do
for j := 0 to GWidth - 1 do begin
tmp := j * param[6] + i * param[7] + param[8];
if tmp = 0 then tmp := 1; // 割り算エラー防止
tmpX := (j * param[0] + i * param[1] + param[2]) / tmp;
tmpY := (j * param[3] + i * param[4] + param[5]) / tmp;
X := Trunc(tmpX);
Y := Trunc(tmpY);
if (X >= 0) and (X < GWidth) and (Y >= 0) and (Y < Gheight) then
OutputBitmap.Canvas.Pixels[j, i] := inputDBitmap.Canvas.Pixels[X, Y]
else
OutputBitmap.Canvas.Pixels[j, i] := clblack;
end;
end;
// ホモグラフィ変換
procedure TForm1.Homography;
var
P : TpMat;
Po : TpMat;
i, J : Integer;
messtr : string;
Param : T8Mat;
inv_param : T9Mat;
pm : T4x4Mat;
begin
// 台形形状取得
for i := 0 to 3 do begin
val(StringGrid1.Cells[1, i + 1], P[i, 0], j);
if J <> 0 then begin
messtr := '上側' + IntTostr(i + 1) + '番目のXの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
val(StringGrid1.Cells[2, i + 1], P[i, 1], j);
if J <> 0 then begin
messtr := '上側' + IntTostr(i + 1) + '番目のYの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
end;
// 出力先ビットマップサイズ
for i := 0 to 3 do begin
val(StringGrid2.Cells[1, i + 1], Po[i, 0], j);
if J <> 0 then begin
messtr := '下側' + IntTostr(i + 1) + '番目のXの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
val(StringGrid2.Cells[2, i + 1], Po[i, 1], j);
if J <> 0 then begin
messtr := '下側' + IntTostr(i + 1) + '番目のYの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
end;
// 変換パラメーター計算
Param := getParam(Po, P);
// 4 x 4 マトリックス
pm[0,0] := param[0]; pm[0,1] := param[1]; pm[0,2] := param[2]; pm[0,3] := 0;
pm[1,0] := param[3]; pm[1,1] := param[4]; pm[1,2] := param[5]; pm[1,3] := 0;
pm[2,0] := param[6]; pm[2,1] := param[7]; pm[2,2] := 1; pm[2,3] := 0;
pm[3,0] := 0; pm[3,1] := 0; pm[3,2] := 0; pm[3,3] := 1;
// 変換の方向変更を逆行列で行います
// Po と P を逆にして変換パラメーターを逆にすれば良いのですがプログラム例として逆行列を使用しています
if checkBox1.Checked then
pm := mat4inverse(pm);
// 変換パラメーターセット
inv_param[0] := pm[0,0];
inv_param[1] := pm[0,1];
inv_param[2] := pm[0,2];
inv_param[3] := pm[1,0];
inv_param[4] := pm[1,1];
inv_param[5] := pm[1,2];
inv_param[6] := pm[2,0];
inv_param[7] := pm[2,1];
inv_param[8] := pm[2,2];
//描画処理
draw(inv_param);
end;
次に8次元連立方程式を8X8行列計算の例をあげます。
こちらのプログラム例は、射影変換のバラメーターを求めるを参考にしました。
逆行列の計算は掃き出し法を使用しました。
掃き出し法は、計算に少し時間が掛かりますが、変換係数の計算時にしか使用されないので、全体の実行時間には大きな影響はありません。
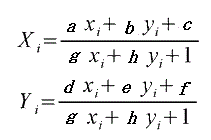 求める座標がXi,Yi の時
求める座標がXi,Yi の時
両辺に分母を払い一次多項式に展開
Xi = xi*a + yi*b + c - xi*g*Xi - yi*h*Xi
Yi = xi*d
+ yi*e + f - xi*g*Yi - yi*h*Yi
変換前の座標 左上から時計回り
(x1,y1),(x2,y2)
(x4,y4),(x3,y3)
変換後の座標 左上から時計回り
(X1,Y1),(X2,Y2)
(X4,Y4),(X3,Y3)
として、
8次元連立一次方程式
X1= x1*a + y1*b + c -
x1*g*X1 - y1*h*X1
X2= x2*a + y2*b + c - x2*g*X2 - y2*h*X2
X3= x3*a + y3*b
+ c - x3*g*X3 - y3*h*X3
X4= x4*a + y4*b + c - x4*g*X4 - y4*h*X4
Y1= x1*d +
y1*e + f - x1*g*Y1 - y1*h*Y1
Y2= x2*d + y2*e + f - x2*g*Y2 - y2*h*Y2
Y3=
x3*d + y3*e + f - x3*g*Y3 - y3*h*Y3
Y4= x4*d + y4*e + f - x4*g*Y4 - y4*h*Y4
として行列式作成
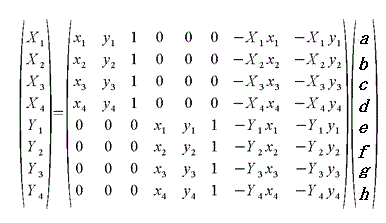
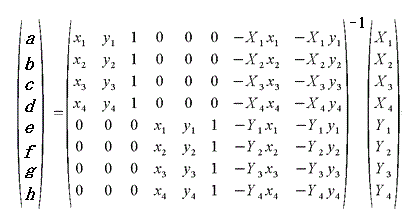
により a~h
を求めれば必要とする座標の計算が出来ることになります。
次の例では、画像を変換するとき、線形補間を利用しています。
線形補間を行う為と変換の高速化の為、画像データーをRGB 三色の二次元配列にしてから、射影変換を行っています。
ピクセル単位で行うと、データーの取り出しと、書き込みに時間がかかり、画像データーが大きいと非常に時間が掛かります。
スキャンラインを使用して、RGBの配列に変換してから射影変換をしたほうが速く変換が出来ます。
サンプルプログラムは此処でダウンロード出来る圧縮ファイルの中のホルダー名 HomographyP、HomographyQ の中にあります。
P
はデーターを取り出すのに、BitMapからPixels単位で取り出し、又、ピクセル単位で書き込みを行っていますが、このモードでは非常にデーターの取り出しと、書き込みに時間が掛かるので、Qでは、二次元配列に変換してから射影の変換をしています。
二次元の配列に変換するのが無駄のように見えますが、Pixels単位での読み書きは非常に時間が掛かるので、変換したほうが計算時間は早くなります。
// 逆行列
function Inverse(n : integer; inpmat: TNmat): TNmat;// 逆行列の作成 掃き出し方 行列
var
invmat: Tnmat;
I , J, k: integer;
nm : integer;
buf : double;
begin
setlength(invmat, n, n);
nm := n - 1;
//単位行列を作る
for i:= 0 to nm do // 対角に1をセット
for j := 0 to nm do
if i = j then invmat[i, j] := 1.0
else invmat[i, j] := 0.0;
//掃き出し法
for i := 0 to nm do
begin
if inpmat[i, i] <> 0 then buf := 1 / inpmat[i, i] // ゼロで除算するのを防止
else buf := 1; // プログラムにミスがなければゼロになりません
for j := 0 to nm do
begin
inpmat[i, j] := inpmat[i, j] * buf;
invmat[i, j] := invmat[i, j] * buf;
end;
for j := 0 to nm do
begin
if i <> j then // 対角でなかったら
begin
buf := inpmat[j, i];
for k := 0 to nm do
begin
inpmat[j, k] := inpmat[j, k] - inpmat[i, k] * buf;
invmat[j, k] := invmat[j, k] - invmat[i, k] * buf;
end;
end;
end;
end;
Result := invmat;
end;
// 変換パラメーター設定
function TForm1.getParam(Sr, Tr: TpMat): T8mat;
var
A, I : TnMat;
Param : T8Mat;
begin
setlength(A, 8, 8);
setlength(I, 8, 8);
// ここの座標の値が等しいと逆行列detの値が0になるので少しずらします。
if Sr[0,1] = Sr[1,1] then Sr[0,1] := Sr[0,1] + 0.1;
A[0,0] := Sr[0,0]; A[0,1] := Sr[0,1]; A[0,2] := 1; A[0,3] := 0;
A[0,4] := 0; A[0,5] := 0; A[0,6] := -Tr[0,0] * Sr[0,0]; A[0,7] := -Tr[0,0] * Sr[0,1];
A[1,0] := Sr[1,0]; A[1,1] := Sr[1,1]; A[1,2] := 1; A[1,3] := 0;
A[1,4] := 0; A[1,5] := 0; A[1,6] := -Tr[1,0] * Sr[1,0]; A[1,7] := -Tr[1,0] * Sr[1,1];
A[2,0] := Sr[2,0]; A[2,1] := Sr[2,1]; A[2,2] := 1; A[2,3] := 0;
A[2,4] := 0; A[2,5] := 0; A[2,6] := -Tr[2,0] * Sr[2,0]; A[2,7] := -Tr[2,0] * Sr[2,1];
A[3,0] := Sr[3,0]; A[3,1] := Sr[3,1]; A[3,2] := 1; A[3,3] := 0;
A[3,4] := 0; A[3,5] := 0; A[3,6] := -Tr[3,0] * Sr[3,0]; A[3,7] := -Tr[3,0] * Sr[3,1];
A[4,0] := 0; A[4,1] := 0; A[4,2] := 0; A[4,3] := Sr[0,0];
A[4,4] := Sr[0,1]; A[4,5] := 1; A[4,6] := -Tr[0,1] * Sr[0,0]; A[4,7] := -Tr[0,1] * Sr[0,1];
A[5,0] := 0; A[5,1] := 0; A[5,2] := 0; A[5,3] := Sr[1,0];
A[5,4] := Sr[1,1]; A[5,5] := 1; A[5,6] := -Tr[1,1] * Sr[1,0]; A[5,7] := -Tr[1,1] * Sr[1,1];
A[6,0] := 0; A[6,1] := 0; A[6,2] := 0; A[6,3] := Sr[2,0];
A[6,4] := Sr[2,1]; A[6,5] := 1; A[6,6] := -Tr[2,1] * Sr[2,0]; A[6,7] := -Tr[2,1] * Sr[2,1];
A[7,0] := 0; A[7,1] := 0; A[7,2] := 0; A[7,3] := Sr[3,0];
A[7,4] := Sr[3,1]; A[7,5] := 1; A[7,6] := -Tr[3,1] * Sr[3,0]; A[7,7] := -Tr[3,1] * Sr[3,1];
// 逆行列
I := Inverse(8, A);
param[0] := I[0,0] * Tr[0,0] + I[0,1] * Tr[1,0] + I[0,2] * Tr[2,0] + I[0,3] * Tr[3,0] +
I[0,4] * Tr[0,1] + I[0,5] * Tr[1,1] + I[0,6] * Tr[2,1] + I[0,7] * Tr[3,1];
param[1] := I[1,0] * Tr[0,0] + I[1,1] * Tr[1,0] + I[1,2] * Tr[2,0] + I[1,3] * Tr[3,0] +
I[1,4] * Tr[0,1] + I[1,5] * Tr[1,1] + I[1,6] * Tr[2,1] + I[1,7] * Tr[3,1];
param[2] := I[2,0] * Tr[0,0] + I[2,1] * Tr[1,0] + I[2,2] * Tr[2,0] + I[2,3] * Tr[3,0] +
I[2,4] * Tr[0,1] + I[2,5] * Tr[1,1] + I[2,6] * Tr[2,1] + I[2,7] * Tr[3,1];
param[3] := I[3,0] * Tr[0,0] + I[3,1] * Tr[1,0] + I[3,2] * Tr[2,0] + I[3,3] * Tr[3,0] +
I[3,4] * Tr[0,1] + I[3,5] * Tr[1,1] + I[3,6] * Tr[2,1] + I[3,7] * Tr[3,1];
param[4] := I[4,0] * Tr[0,0] + I[4,1] * Tr[1,0] + I[4,2] * Tr[2,0] + I[4,3] * Tr[3,0] +
I[4,4] * Tr[0,1] + I[4,5] * Tr[1,1] + I[4,6] * Tr[2,1] + I[4,7] * Tr[3,1];
param[5] := I[5,0] * Tr[0,0] + I[5,1] * Tr[1,0] + I[5,2] * Tr[2,0] + I[5,3] * Tr[3,0] +
I[5,4] * Tr[0,1] + I[5,5] * Tr[1,1] + I[5,6] * Tr[2,1] + I[5,7] * Tr[3,1];
param[6] := I[6,0] * Tr[0,0] + I[6,1] * Tr[1,0] + I[6,2] * Tr[2,0] + I[6,3] * Tr[3,0] +
I[6,4] * Tr[0,1] + I[6,5] * Tr[1,1] + I[6,6] * Tr[2,1] + I[6,7] * Tr[3,1];
param[7] := I[7,0] * Tr[0,0] + I[7,1] * Tr[1,0] + I[7,2] * Tr[2,0] + I[7,3] * Tr[3,0] +
I[7,4] * Tr[0,1] + I[7,5] * Tr[1,1] + I[7,6] * Tr[2,1] + I[7,7] * Tr[3,1];
result := param;
end;
// 変換画像作成
procedure TForm1.draw(param: T8Mat);
var
R, G, B : array[0..1] of array[0..1] of byte;
i, j, k, l : Integer;
tmp : double;
tmpX, tmpY : Double;
X, Y : Integer;
dX, dY : Double;
MdX, MdY : Double;
PB : Pbytearray;
begin
for i := 0 to Gheight - 1 do
for j := 0 to GWidth - 1 do begin
tmp := j * param[6] + i * param[7] + 1;
if tmp = 0 then tmp := 1; // ゼロで除算するのを防止 プログラムにミスがなければゼロになりません
tmpX := (j * param[0] + i * param[1] + param[2]) / tmp;
tmpY := (j * param[3] + i * param[4] + param[5]) / tmp;
X := floor(tmpX); // 負の方向へまるめ 此処ではゼロ以下は使用しないのでTruncでもOk
Y := floor(tmpY);
dX := tmpX - X;
dY := tmpY - Y;
// 線形補間
if (X >= 0) and (X < GWidth - 1) and (Y >= 0) and (Y < Gheight - 1) then begin
for k := 0 to 1 do
for l := 0 to 1 do begin
R[k, l] := InpRmat[X + k, Y + l];
G[k, l] := InpGmat[X + k, Y + l];
B[k, l] := InpBmat[X + k, Y + l];
end;
MdX := 1 - dX;
MdY := 1 - dY;
OutRmat[j, i] := Trunc(MdX * (MdY * R[0, 0] + dY * R[0, 1]) + dX * (MdY * R[1, 0] + dY * R[1, 1]));
OutGmat[j, i] := Trunc(MdX * (MdY * G[0, 0] + dY * G[0, 1]) + dX * (MdY * G[1, 0] + dY * G[1, 1]));
OutBmat[j, i] := Trunc(MdX * (MdY * B[0, 0] + dY * B[0, 1]) + dX * (MdY * B[1, 0] + dY * B[1, 1]));
end
else begin
OutRmat[j, i] := 0;
OutGmat[j, i] := 0;
OutBmat[j, i] := 0;
end;
end;
for Y := 0 to Gheight - 1 do begin
PB := OutputBitmap.ScanLine[Y];
for X := 0 to GWidth - 1 do begin
k := X * 4;
PB[k ] := OutBmat[X, Y];
PB[k + 1] := OutGmat[X, Y];
PB[k + 2] := OutRmat[X, Y];
PB[k + 3] := 0;
end;
end;
end;
// ホモグラフィ変換
procedure TForm1.Homography;
var
P : TpMat;
Po : TpMat;
i, J : Integer;
messtr : string;
Param : T8Mat;
begin
// 台形形状取得
for i := 0 to 3 do begin
val(StringGrid1.Cells[1, i + 1], P[i, 0], j);
if J <> 0 then begin
messtr := '上側' + IntTostr(i + 1) + '番目のXの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
val(StringGrid1.Cells[2, i + 1], P[i, 1], j);
if J <> 0 then begin
messtr := '上側' + IntTostr(i + 1) + '番目のYの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
end;
// 出力先ビットマップサイズ
for i := 0 to 3 do begin
val(StringGrid2.Cells[1, i + 1], Po[i, 0], j);
if J <> 0 then begin
messtr := '下側' + IntTostr(i + 1) + '番目のXの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
val(StringGrid2.Cells[2, i + 1], Po[i, 1], j);
if J <> 0 then begin
messtr := '下側' + IntTostr(i + 1) + '番目のYの値にミスがあります。';
application.MessageBox(Pchar(messtr),'注意',0);
exit;
end;
end;
// 変換パラメーター計算 変換方向入れ替え
if checkBox1.Checked then
Param := getParam(Po, P)
else
Param := getParam(P, Po);
//描画処理
draw(param);
end;

上図の例は、左の画像の四箇所の頂点を指定して、右側の画像の頂点の位置へ変換をしています。
右の画像を左の画像へも変換が可能です。
入力と出力の入れ替えは、逆マトリックスを行うか行わないか、又は、パラメーターの計算時、四箇所の指定点を、入力側と出力側入れ替えて行います。
Delphiの中のFireMonkeyに、透視変換効果'(PerspectiveTransformEffect)があるのですが、四点を指定して、変換をしているので、ホモグラフィ変換だと思われます。
procedure TForm1.Button1Click(Sender: TObject);
begin
PerspectiveTransformEffect1.TopLeft := PointF(100, 0);
PerspectiveTransformEffect1.TopRight := PointF(200, 0);
PerspectiveTransformEffect1.BottomLeft := PointF( 0,300);
PerspectiveTransformEffect1.BottomRight := PointF(300,300);
end;
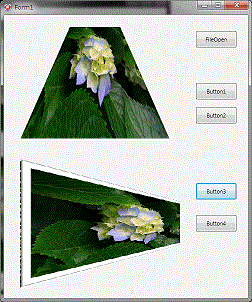
単に、指定された四点の形状で表示を行うだけで、画像データーの変換出力は出来ないようです。
サンプルプログラムは、ホルダー FMXPerspective の中にあります。
此処でダウンロード出来るプログラムの中に、色々な場合の組み合わせについて作成してあります。
一応全て実行確認はされています。
 homography.zip
homography.zip
画像処理一覧へ戻る
最初に戻る


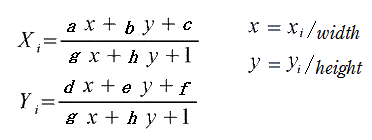 となっているようです。
となっているようです。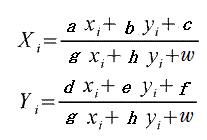 となります。
となります。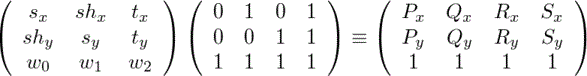
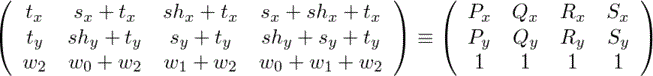
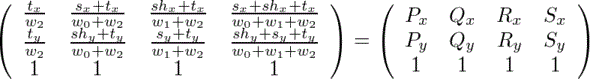
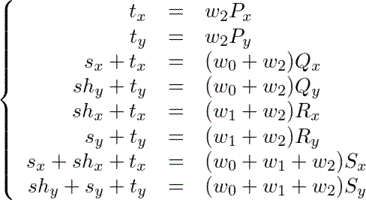
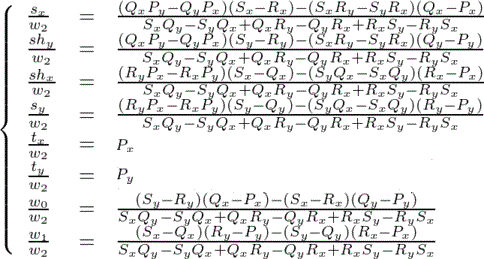
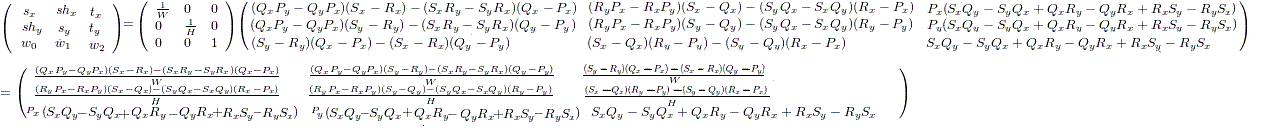
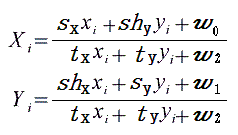

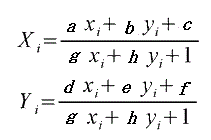 求める座標がXi,Yi の時
求める座標がXi,Yi の時