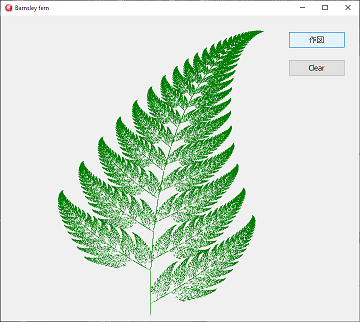
作図ボタンでシダが描画されClearボタンで消去される簡単なプログラムです。FormのCanvasに直接描画しているので最小化して、再度表示すると、画像が消去されます。
消去されないようにする場合は、Tbitmapに描画する必要があります。
フラクタル図形のシダ
フラクタル図形のシダにバーンズリーのシダ（Barnsley fern）がウィキペディア（Wikipedia）に記載されており、プログラム例があったので、Delphiで作成してみました。
作図ボタンでシダが描画されClearボタンで消去される簡単なプログラムです。
FormのCanvasに直接描画しているので最小化して、再度表示すると、画像が消去されます。
消去されないようにする場合は、Tbitmapに描画する必要があります。
上図のプログラム
unit Unit1;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Button2: TButton;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
private
{ Private 宣言 }
procedure fern;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
procedure TForm1.fern;
const
xpos = 300; // 作図開始座標 X
ypos = 600; // 作図開始座標 y
var
x, y, xn, yn, r: double;
n: integer;
xi, yi: integer;
begin
x := 0;
y := 0;
for n := 0 to 200000 do begin
r := random; // 0 <= r < 1
xn := x;
yn := y;
if r < 0.01 then begin // 1％
x := 0;
y := 0.16 * yn;
end
else
if r < 0.86 then begin // 85％
x := 0.85 * xn + 0.04 * yn;
y := -0.04 * xn + 0.85 * yn + 1.6;
end
else
if r < 0.93 then begin // 7％
x := 0.20 * xn - 0.26 * yn;
y := 0.23 * xn + 0.22 * yn + 1.6;
end
else begin // 7％
x := -0.15 * xn + 0.28 * yn;
y := 0.26 * xn + 0.24 * yn + 0.44;
end;
xi := round(85 * x + xpos); // 85はx方向の倍率
yi := round(ypos - 57 * y); // 57はy方向の倍率
canvas.Pixels[xi, yi] := clGreen;
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
Button1.Enabled := False;
fern;
Button1.Enabled := True;
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
canvas.Brush.Color := clbtnface;
canvas.FillRect(rect(0, 0, width, height));
end;
end.
シダ + その他 のフラクタル図形例
プログラム
最初の旧シダのプログラムと、前記のシダのプログラムは、計算手法は違いますが、内容的には同じです。
unit Unit1;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Image1: TImage;
RadioGroup1: TRadioGroup;
Button1: TButton;
procedure Button1Click(Sender: TObject);
private
{ Private 宣言 }
procedure pteridophytes;
public
{ Public 宣言 }
end;
var
Form1: TForm1;
implementation
uses System.math;
{$R *.dfm}
procedure TForm1.pteridophytes;
var
N, M : integer;
Q : Cardinal;
a, b, c, d, e, f, p : array of double;
i, j, k, r : integer;
ip, table : array of integer;
x, y, s, t : double;
xi, yi : integer;
xs, ys : double;
xb, yb : integer;
select : byte;
Pcolor : Tcolor;
begin
// 画像クリア
Image1.canvas.Brush.Color := clBtnface;
Image1.canvas.fillrect(rect(0, 0, Image1.Width, Image1.Height));
// 作図選択
select := RadioGroup1.ItemIndex;
// Barnsley fern classic version
// select = 0
N := 4; // データー配列の大きさ
xs := 60; // 表示Xスケール
ys := 35; // 表示Yスケール
xb := 230; // 画像x位置
yb := 370; // 画像y位置
Q := 80000; // プロット数
Pcolor := clGreen; // プロット色
// Barnsley fern
if select = 1 then begin
N := 4;
xs := 100;
ys := 60;
xb := 250;
yb := 380;
Q := 100000;
Pcolor := clGreen;
end;
// ヒメシダ Thelypteridaceae fern
if select = 2 then begin
N := 4;
xs := 120;
ys := 48;
xb := 250;
yb := 360;
Q := 200000;
Pcolor := clGreen;
end;
// Sierpinskiの三角形
if select = 3 then begin
N := 3;
xs := 200;
ys := 320;
xb := 50;
yb := 350;
Q := 30000;
Pcolor := clBlue;
end;
// 簡単な木
if select = 4 then begin
N := 4;
xs := 700;
ys := 800;
xb := 250;
yb := 430;
Q := 100000;
Pcolor := clRed;
end;
// 詳細な木
if select = 5 then begin
N := 6;
xs := 230;
ys := 150;
xb := 250;
yb := 370;
Q := 100000;
Pcolor := clBlack;
end;
// 配列の確保
M := N * 25; // Mの値は一番小さい確率に合わせます
setlength(a, N);
setlength(b, N);
setlength(c, N);
setlength(d, N);
setlength(e, N);
setlength(f, N);
setlength(p, N);
setlength(ip, N);
setlength(table, M);
// Barnsley fern classic version
if select = 0 then begin
// シダの茎 連続する小さい葉 左の葉 右の葉
a[0] := 0.00; a[1] := 0.85; a[2] := 0.2 ; a[3] :=-0.15;
b[0] := 0.00; b[1] := 0.04; b[2] :=-0.26; b[3] := 0.28;
c[0] := 0.00; c[1] :=-0.04; c[2] := 0.23; c[3] := 0.26;
d[0] := 0.16; d[1] := 0.85; d[2] := 0.22; d[3] := 0.24;
e[0] := 0.00; e[1] := 0.00; e[2] := 0.00; e[3] := 0.00;
f[0] := 0.00; f[1] := 1.60; f[2] := 1.60; f[3] := 0.44;
p[0] := 0.05; p[1] := 0.85; p[2] := 0.10; p[3] := 0.1; // 確率
end;
// Barnsley fern
if select = 1 then begin
// シダの茎 連続する小さい葉 左の葉 右の葉
a[0] := 0 ; a[1] := 0.85; a[2] := 0.09; a[3] :=-0.09 ;
b[0] := 0 ; b[1] := 0.02; b[2] :=-0.28; b[3] := 0.28;
c[0] := 0 ; c[1] :=-0.02; c[2] := 0.3 ; c[3] := 0.3 ;
d[0] := 0.25; d[1] := 0.83; d[2] := 0.11; d[3] := 0.09;
e[0] := 0 ; e[1] := 0 ; e[2] := 0 ; e[3] := 0 ;
f[0] :=-0.14; f[1] := 1 ; f[2] := 0.6 ; f[3] := 0.7 ;
p[0] := 0.02; p[1] := 0.84; p[2] := 0.07; p[3] := 0.07;
end;
// ヒメシダ Thelypteridaceae fern
if select = 2 then begin
// シダの茎 連続する小さい葉 左の葉 右の葉
a[0] := 0 ; a[1] := 0.95 ; a[2] := 0.035; a[3] :=-0.04;
b[0] := 0 ; b[1] := 0.005; b[2] :=-0.2 ; b[3] := 0.2 ;
c[0] := 0 ; c[1] :=-0.005; c[2] := 0.16 ; c[3] := 0.16;
d[0] := 0.25; d[1] := 0.93 ; d[2] := 0.04 ; d[3] := 0.04;
e[0] := 0 ; e[1] :=-0.002; e[2] :=-0.09 ; e[3] := 0.083;
f[0] :=-0.4 ; f[1] := 0.5 ; f[2] := 0.02 ; f[3] := 0.12 ;
// p[0] := 0.02; p[1] := 0.84 ; p[2] := 0.07 ; p[3] := 0.07; // Q>5000000
p[0] := 0.02; p[1] := 0.87 ; p[2] := 0.04 ; p[3] := 0.04; // Q= 300000
end;
// Sierpinskiの三角形
if select = 3 then begin
a[0] := 0.5; a[1] := 0.5; a[2] := 0.5;
b[0] := 0 ; b[1] := 0 ; b[2] := 0 ;
c[0] := 0 ; c[1] := 0 ; c[2] := 0 ;
d[0] := 0.5; d[1] := 0.5; d[2] := 0.5;
e[0] := 0 ; e[1] := 1 ; e[2] := 0.5;
f[0] := 0 ; f[1] := 0 ; f[2] := 0.5;
end;
// 簡単な木
if select = 4 then begin
a[0] := 0 ; a[1] := 0.1 ; a[2] := 0.42; a[3] := 0.42;
b[0] := 0 ; b[1] := 0 ; b[2] :=-0.42; b[3] := 0.42;
c[0] := 0 ; c[1] := 0 ; c[2] := 0.42; c[3] :=-0.42;
d[0] := 0.5; d[1] := 0.1 ; d[2] := 0.42; d[3] := 0.42;
e[0] := 0 ; e[1] := 0 ; e[2] := 0 ; e[3] := 0 ;
f[0] := 0 ; f[1] := 0.2 ; f[2] := 0.2 ; f[3] := 0.2 ;
end;
// 詳細な木
if select = 5 then begin
a[0] := 0.05; a[1] := 0.05; a[2] := 0.46; a[3] := 0.47; a[4] := 0.43; a[5] := 0.42;
b[0] := 0 ; b[1] := 0 ; b[2] :=-0.32; b[3] :=-0.15; b[4] := 0.28; b[5] := 0.26;
c[0] := 0 ; c[1] := 0 ; c[2] := 0.39; c[3] := 0.17; c[4] :=-0.25; c[5] :=-0.35;
d[0] := 0.6 ; d[1] :=-0.5 ; d[2] := 0.38; d[3] := 0.42; d[4] := 0.45; d[5] := 0.31;
e[0] := 0 ; e[1] := 0 ; e[2] := 0 ; e[3] := 0 ; e[4] := 0 ; e[5] := 0 ;
f[0] := 0 ; f[1] := 1 ; f[2] := 0.6 ; f[3] := 1.1 ; f[4] := 1 ; f[5] := 0.7 ;
end;
s := 0;
// 確率の計算
for i := 0 to N - 1 do begin
if select > 2 then // シダ以外
p[i] := abs(a[i] * d[i] - b[i] * c[i]); // 確率計算
s := s + p[i];
ip[i] := i;
end;
// 表作成 確率に合わせた数の出現配列テーブル作成
r := M;
for i := 0 to N - 1 do begin
k := trunc(r * p[i] / s + 0.5);
s := s - p[i];
repeat
dec(r);
table[r] := ip[i];
dec(k);
until k <= 0;
end;
// プロット テーブルからランダムにa～f配列Noを取り出して座標を計算プロットします
y := 0;
x := 0;
for i := 0 to Q do begin
j := table[random(M)]; // a～f配列Noをランダムに取り出す
t := a[j] * x + b[j] * y + e[j];
y := c[j] * x + d[j] * y + f[j];
x := t;
xi := xb + round(x * xs);
yi := yb - round(y * ys);
// if i > 10 then // 計算開始頃のxi,yi値は近似値となり易いので避ける場合があります
// Qの値が大きいので無視をしても良いかと思います。
Image1.canvas.Pixels[xi, yi] := Pcolor;
end;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
Button1.Enabled := False;
pteridophytes;
Button1.Enabled := True;
end;
end.
Fractal_V01.zip
画像処理プログラム 作図 に戻る