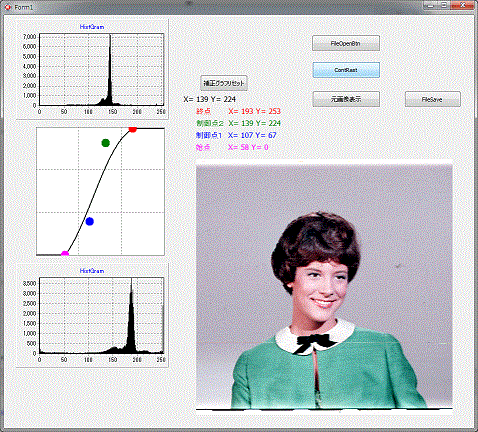
コントラストの調整

コントラストの調整は、ガンマ補正で調整できますが、S型曲線と、自由曲線による補正を行ってみました。
S型曲線は、シグモイド曲線を使用し、自由曲線は、ベジェ曲線を使用します。
シグモイド曲線によるコントラスト調整
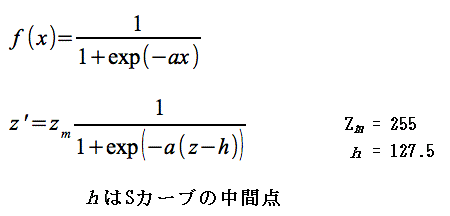
左はシグモイド関数です。
画像データーは、0~255なので、Sカーブの中間点は、127.5となります。
このまヽでは、使いづらいので、少し変更します。
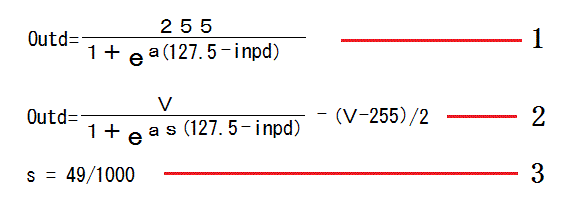
1は単純にaのマイナスの符号を取っただけです。
このまヽでは、aの値が非常に小さくなって扱いづらいので、係数S=0.049を乗じてaの値を約1の値になるようにします。
更に、カーブの角度が変えられるように、Vの変数項を追加します。
この場合、255以上の値をVに与えると、計算結果に、0以下と255以上が現れるので、0以下は0とし、255以上は、255に制限するようにします。
実際には、更に、横シフト、縦シフトを追加して、元図のヒストグラムにあわせることが出来る様にして使用します。

aの値はGainとし、Vの値は、曲線係数です。

シフトすることにより、立ち上がり点、終点近傍のカーブをある程度自由なカーブを与えることが可能です。
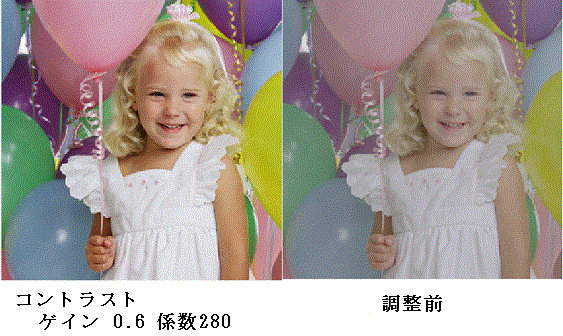

gainにマイナスの値を与えると、画像が反転します。
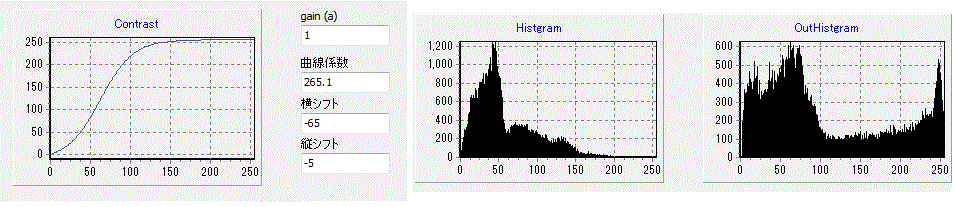
次に画像の輝度ヒストグラムをみてみましょう。
ヒストグラムは、グレーの輝度に変換して表示しています。

左側のヒストグラムが、修正前のヒストグラムですが、グラフにある曲線でコントラストの補正を行うと、右側のヒストグラムの状態に補正されます。
グラフが、広がっているのが分かります。
補正の結果上図の様に明るい画像に修正されます。
シグノイド曲線の適用はここでも計算を早くする為、テンプレートを使用します。
テンプレートは、配列を使用し、変換テーブル作成しをそれを使用ます。
元画像のデーターを配列の添え字とすると、配列の値が変換後の値となり、演算不要で値を変換することができます。
データーの変換は、1つの座標に対して、カラーなので三回変換が行われるだけなので、高速に処理が終了します。
ベジェ曲線によるコントラスト補正
シグノイド曲線を使用する場合、目的の曲線を得るのに、係数を何度も修正しないと、良い結果が得られません。
それに対して、グラフの曲線を容易に変更できるベジェ曲線を使用してみました。
ベジェ曲線は、次の式であらわされます。
(x1,y1)始点
(x2,y2)制御点1
(x3,y3)制御点2
(x4,y4)終点
x = x(t) = t^3*x4 + 3*t^2*(1-t)*x3 + 3*t*(1-t)^2*x2 +
(1-t)^3*x1
y = y(t) = t^3*y4 + 3*t^2*(1-t)*y3 + 3*t*(1-t)^2*y2 + (1-t)^3*y1
t の値を 0 から 1 迄変化させ描画することで、ベジェ曲線を得ることが出来ます。
始点から終点の値は、0~255の値を、始点、制御点1、制御点2、終点の座標に与えれば、0~255の曲線になります。
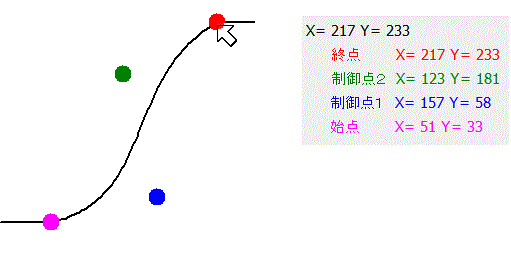
制御点を与える方法として、ここのプログラムでは、グラフ上の点をマウスで移動することに、制御点を設定することが出来ます。
始点のX1座標が0より大きい場合は、0から始点座標X1迄のYの値は、Y1とし、終点のX4座標が255以下の場合は、X4から255迄のYの値はY4の値を使用します。
ベジェ曲線は、あくまでも、始点から終点の間だけです。
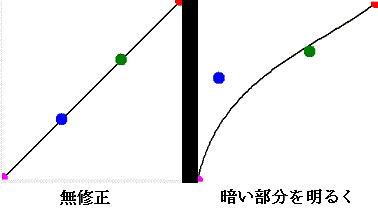

ベジェ曲線にも補正テンプレートを使用します。
テンプレートとして配列変換テーブルを作成しますが、シグモイドと違ってベジェ曲線の変換テーブルの作成には工夫が必要です。
三種類の変換テーブルの作成方法を検討してみました。
1 ベジェ曲線を作図し、曲線図を読み取る方法
簡単な方法としては、ベジェ曲線のグラフを描画し、グラフの線の位置を読み取ってテーブルを作成する方法です。
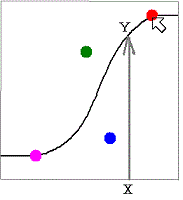
グラフX軸 0~255 の間のYの値を読み取ります。
その為に、横軸と縦軸のドット数が256になるように作図をしておきます。
制御点を移動して、制御点の位置を取得するのにも便利です。
グラフの線か、制御点の丸かの判別は、その点のピクセルの値で色で判別します、その為読み取る瞬間は、読み取る色で最後にグラフに曲線を描画して、読み取り後、制御点を描画して、制御点の移動に備えます。
2 ⊿tの値を小さくとり、X、Yの値を計算し配列に書き込む方法
グラフに書き込む代わりに、テーブル配列に直接書き込む方法もあります。
配列に直接書き込む時は、配列のデーターを一度、使用されない値で、初期化し、書き込む時に書き込み済みかどうか判別、書き込みしていなかったら書き込むようにすることで配列テーブルが作成できます。
通常は、値が0~255なので、配列は
Byte(8ビット)の配列を用意しますが、書き込んだかどうかの判別をする為、SmallInt(符号付16ビット)を使用します。
その時の注意点としては、計算するベジェ曲線の⊿tの値を十分小さくして、配列テーブルの値に抜けが無いようにします。
⊿t の値は0.001以下に設定すれば、データーの抜けは無くなるようです。
ベジェ曲線の制御点は、グラフの枠内何処えでも移動可能なので、次のような条件を設定してしまう場合があり注意して下さい、実際に移動すると、次の例よりももっと異常な曲線にもなります。
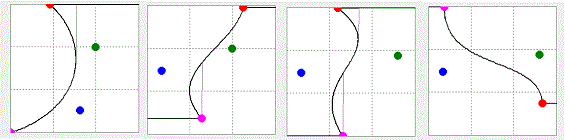
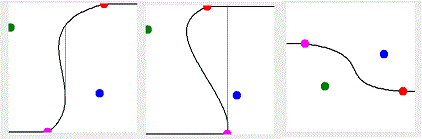
グラフから、値を読み取る場合、或いは、⊿t によりグラフを作成すると、テーブルの値は、曲線と、細い直線で繋がった値となります。
通常は使用しない曲線です。
Xの値は一旦右へ行って、戻る事は出来ません、その為、その上の曲線、又は直線と接する点が、テーブルの値となります、右から二番目の状態は、縦の直線の位置で、2値化をするのと同じ意味です。
3 Xの値から t の値を求め t からYの値を求める方法
次に、制御点を与え、t の値で、XとYの値を得るのではなく、Xの値から、t の値を計算し、更に t からYの値を得る方法を検討してみました。
三次方程式の解の使用です。
x1、x2、x3、x4 では分かりづらいので、a、b、c、dに置き換えます。
x=a(1-t)^3 +
b(3t(1-t)^2)+c(3t^2(1-t))+dt^3
のベジェの t から X値を計算する式から、t を求められる形に変換します。
x = a-3at+3at^2-at^3+3bt-6bt^2+3bt^3+3ct^2-3ct^3+dt^3
=
a-3at+3bt+3at^2-6bt^2+3ct^2-at^3+3bt^3-3ct^3+dt^3
=
a+(3b-3a)t+(3a-6b+3c)t^2+(3b-a-3c+d)t^3
t でまとめると
a+(3b-3a)t+(3a-6b+3c)t^2+(3b-a-3c+d)t^3-x = 0
これで、三次方程式となったので、t の値を求められます。
(3b-a-3c+d)t^3 + (3a-6b+3c)t^2 +
(3b-3a)t + a - x = 0
a,b,c,d,xは、既知数なので、
a0 = 3b-a-3c+d
a1 = 3a-6b+3c
a2 = 3b-3a
a3 = a - x;
とし、
a0t^3+a1t^2+a3t+d = 0 但し a0 がゼロではいけない。
の t
の値を本プログラムでは、カルダノの方法で求めます。
カルダノの方法の解説については、他のホームページを検索してで参照願います。
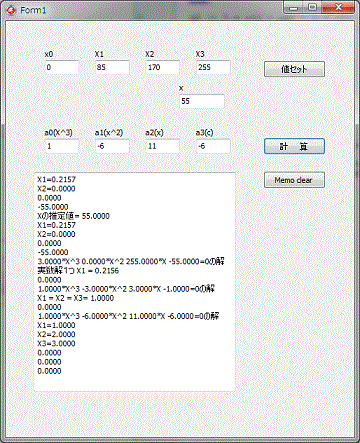
カルダノの三次方程式をコントラスト調整プログラムに組み込む前に、方程式の解を求める部分だけのプログラムを作りました。
X0、X1、X2、X3にベジェ曲線の制御数値 X側の値を入れます。
Xには、X軸の値です。
”値セット”ボタンをクリックすれば、a0、a1、a2、a3の値をセットし、三次元方程式の解を求め、答えが正しいか三次方程式を計算し正しければゼロが出力されます。
プログラムを組む上での注意点としてまず、立方根があります。
立方根は power(X,1/3)
ですが、Xの値が負数であるとエラーになります、しかし、負数の三乗は負数であるので、一旦符号を取って立方根を求め、改めて負数にします。
次に arcTan
は、四象限の角度が求められる arctan2(Y, X)を使用します。
単にarcTan(X)が、プログラムに使用されていて、象限を求めるようになっていない、三次方程式の解を求めるプログラムは間違いです。
次に、ベジェ曲線の制御点には特異点があります。
円が楕円の特異点であるのと同じです。
四個の制御点の値が、等分に並んだ場合に特異点となります。
例 x1 x2 x3 x4
0 1 2 3
0 3 6 9
1 2 3 4
0 85 170 255
55 110 165 220
この場合は、一次曲線となります、等間隔で無い場合は三次曲線、又は二次曲線になります。
上記値をセットすると、三次曲線のa0とa1の値にゼロが割り付けられるので、一次方程式になる事が分かります。
0 140 225 255
0 136 221 255
0 113 198 255
0 86
171 255
をセットすると a0 にゼロが割り付けられ 二次曲線になります。
unit cmain;
interface
uses
Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,
Vcl.Controls, Vcl.Forms, Vcl.Dialogs, system.Math, Vcl.StdCtrls, Vcl.ExtCtrls;
type
TForm1 = class(TForm)
Memo1: TMemo;
Button1: TButton;
a0Edit: TLabeledEdit;
a1Edit: TLabeledEdit;
a2Edit: TLabeledEdit;
a3Edit: TLabeledEdit;
Button2: TButton;
x0Edit: TLabeledEdit;
X1Edit: TLabeledEdit;
X2Edit: TLabeledEdit;
X3Edit: TLabeledEdit;
Button3: TButton;
xEdit: TLabeledEdit;
procedure FormCreate(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
private
{ Private 宣言 }
procedure Main;
procedure printComplex; // 1実根
procedure printZero; // 等根
procedure PrintReal; // 3実根の出力
procedure quadratic; // 二次方程式と一次方程式の解
public
{ Public 宣言 }
function cubicroot(a :double): double; // 立方根
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
var
a, b, c : double;
a0, a1, a2, a3 : double;
p, q, d2, d : double;
ang3, cc, u3 : double;
v1, u1 : double;
ss, r : double;
ang : double;
x1, x2, x3 : double;
x01, x11, x21, x31 : double;
//***********************************************************
// 立方根を求めます
// Xの1/3乗は負の値は計算出来ないので正の値として計算しますが
// 負数の三乗は負数となるので、元の値が負だったら立方根計算後
// 負の値にします。
//***********************************************************
function TForm1.cubicroot(a :double): double; // 立方根
begin
result := power(abs(a), 1 / 3) * sign(a);
end;
//******************************************
// 実数解は1つです
// あとは虚数となります。
//******************************************
procedure TForm1.printComplex; // 1実根
var
outText : string;
begin
u3 := (q + d) / 2;
u1 := cubicroot(u3);
u3 := (d - q) / 2;
v1 := cubicroot(u3);
x1 := u1 - v1 - a / 3;
outText := '実数解1つ X1 = ' + floatTostrf(x1, ffFixed, 10, 4);
Form1.Memo1.Lines.Add(outText);
end;
//*********************************************
// 三個とも同じ値になります。
//*********************************************
procedure TForm1.printZero; // 等根
var
outText : string;
begin
x1:= cubicroot(4 * q) - a / 3;
outText := 'X1 = X2 = X3= ' + floatTostrf(x1, ffFixed, 10, 4);
Form1.Memo1.Lines.Add(outText);
end;
//*******************************************
// 三個実数の答えがでます。
//*******************************************
procedure TForm1.PrintReal; // 3実根の出力
var
outText : string;
tmp : double;
xa : array[0..2] of double;
II, JJ : integer;
begin
ang3 := arctan2(d, q);
ang := ang3 / 3;
cc := cos(ang);
ss := sin(ang);
r := sqrt(abs(p));
xa[0] := r * ( cc + cc) - a / 3;
xa[1] := r * (-cc - sqrt(3) * ss) - a / 3;
xa[2] := r * (-cc + sqrt(3) * ss) - a / 3;
for JJ := 0 to 1 do // 小さい順に並び替え
for II := 0 to 1 do
if xa[II] > xa[II + 1] then begin
tmp := xa[II + 1];
xa[II + 1] := xa[II];
xa[II] := tmp;
end;
x1 := xa[0];
x2 := xa[1];
x3 := xa[2];
outText := 'X1=' + floatTostrf(x1, ffFixed, 10, 4);
Form1.Memo1.Lines.Add(outText);
outText := 'X2=' + floatTostrf(x2, ffFixed, 10, 4);
Form1.Memo1.Lines.Add(outText);
outText := 'X3=' + floatTostrf(x3, ffFixed, 10, 4);
Form1.Memo1.Lines.Add(outText);
end;
//*************************************
// 結果条件の判別と各ルーチンの処理
//*************************************
procedure TForm1.Main;
var
outtext: string;
ZZ : Double;
begin
outtext := floatTostrF(a0,ffFixed,10,4) + '*X^3 ' + floatTostrF(a1,ffFixed,10,4)
+ '*X^2 ' + floatTostrF(a2,ffFixed,10,4) + '*X ' + floatTostrF(a3,ffFixed,10,4) + '=0の解';
Form1.Memo1.Lines.Add(outText);
p := a * a / 9 - b / 3;
q := -2 * a * a * a / 27 + a * b / 3 - c;
d2 := q * q - 4 * p * p * p; // 判定値計算
d := sqrt(abs(d2));
if d2 > 0 then printComplex; // 1実根
if d2 = 0 then printZero; // 等根
if d2 < 0 then PrintReal; // 3実根の出力
zz := a0 * x1 * X1 * x1 + a1 * x1 * x1 + a2 * x1 + a3; // x1による検算
outtext := floatTostrF(zz,ffFixed,10,4);
Form1.Memo1.Lines.Add(outText);
if d2 < 0 then begin
zz := a0 * x2 * X2 * x2 + a1 * x2 * x2 + a2 * x2 + a3; // x2による検算
outtext := floatTostrF(zz,ffFixed,10,4);
Form1.Memo1.Lines.Add(outText);
zz := a0 * x3 * x3 * x3 + a1 * x3 * x3 + a2 * x3 + a3; // x3による検算
outtext := floatTostrF(zz,ffFixed,10,4);
Form1.Memo1.Lines.Add(outText);
end;
end;
//****************************************
// 三次方程式の解を求めます
//****************************************
procedure TForm1.Button1Click(Sender: TObject);
var
ch : integer;
begin
val(a0edit.Text, a0, ch);
if ch <> 0 then begin
application.MessageBox('a0に入力ミスがあります。','注意',0);
exit;
end;
if a0 = 0 then begin
application.MessageBox('a0がゼロではいけません。','注意',0); // ゼロである注意のみで計算は続行
end;
val(a1edit.Text, a1, ch);
if ch <> 0 then begin
application.MessageBox('a1に入力ミスがあります。','注意',0);
exit;
end;
val(a2edit.Text, a2, ch);
if ch <> 0 then begin
application.MessageBox('a2に入力ミスがあります。','注意',0);
exit;
end;
val(a3edit.Text, a3, ch);
if ch <> 0 then begin
application.MessageBox('a3に入力ミスがあります。','注意',0);
exit;
end;
if a0 = 0 then begin
a := a1;
b := a2;
c := a3;
quadratic; // 二次方程式の解
exit;
end;
a := a1 / a0;
b := a2 / a0;
c := a3 / a0;
Main;
end;
//********************************
// 表示消去
//********************************
procedure TForm1.Button2Click(Sender: TObject);
begin
memo1.Clear;
end;
//***********************************
// 二次方程式と一次方程式の解
//***********************************
procedure TForm1.quadratic; // 二次方程式の解
var
xc0 : double;
outtext: string;
ZZ : Double;
begin
xc0 := b * b - 4 * a * c;
if a <> 0 then begin
if xc0 < 0 then begin // 解なし
x1 := 0;
x2 := 0;
end
else begin
x1 := (-b + sqrt(xc0)) / 2 / a;
x2 := (-b - sqrt(xc0)) / 2 / a;
end;
end
else // a = 0 の場合は一次方程式
begin
x1 := - c / b;
x2 := 0;
end;
outText := 'X1=' + floatTostrf(x1, ffFixed, 10, 4);
Form1.Memo1.Lines.Add(outText);
outText := 'X2=' + floatTostrf(x2, ffFixed, 10, 4);
Form1.Memo1.Lines.Add(outText);
zz := a0 * x1 * X1 * x1 + a1 * x1 * x1 + a2 * x1 + a3; // x1による検算
outtext := floatTostrF(zz,ffFixed,10,4);
Form1.Memo1.Lines.Add(outText);
zz := a0 * x2 * X2 * x2 + a1 * x2 * x2 + a2 * x2 + a3; // x2による検算
outtext := floatTostrF(zz,ffFixed,10,4);
Form1.Memo1.Lines.Add(outText);
end;
//***************************************************
// ベジェ曲線制御値とX又はYの値から制御変数 t の
// 値を求めます。
//***************************************************
procedure TForm1.Button3Click(Sender: TObject);
var
x : double;
ch : integer;
a0,a1,a2,a3 : double;
xxt : double;
begin
val(xedit.Text, x, ch);
if ch <> 0 then begin
application.MessageBox('xに入力ミスがあります','注意',0);
exit;
end;
val(x0edit.Text, x01, ch);
if ch <> 0 then begin
application.MessageBox('x0に入力ミスがあります','注意',0);
exit;
end;
val(x1edit.Text, x11, ch);
if ch <> 0 then begin
application.MessageBox('x1に入力ミスがあります','注意',0);
exit;
end;
val(x2edit.Text, x21, ch);
if ch <> 0 then begin
application.MessageBox('x2に入力ミスがあります','注意',0);
exit;
end;
val(x3edit.Text, x31, ch);
if ch <> 0 then begin
application.MessageBox('x3に入力ミスがあります','注意',0);
exit;
end;
a0 := 3 * x11 - x01 - 3 * x21 + x31;
a1 := 3 * x01 - 6 * x11 + 3 * x21;
a2 := 3 * x11 - 3 * x01;
a3 := x01 - x;
a0edit.Text := floatTostr(a0);
a1edit.Text := floatTostr(a1);
a2edit.Text := floatTostr(a2);
a3edit.Text := floatTostr(a3);
Button1Click(nil);
xxt := x01*power(1-x1,3)+x11*(3*x1*power(1-x1,2))+x21*(3*x1*X1*(1-x1))+x31*x1*x1*x1;
memo1.Lines.Add('Xの推定値= ' + floatTostrf(xxt, ffFixed, 10, 4));
end;
//********************************
// 初期設定
//********************************
procedure TForm1.FormCreate(Sender: TObject);
begin
memo1.Clear;
a0edit.Text := '1.0';
a1edit.Text := '-2.0';
a2edit.Text := '-11.0';
a3edit.Text := '12';
end;
end.
a0がゼロで無い場合は、三次方程式です。
三次方程式の場合、得られる解は、1つの実根と二つの虚数、3個の実根、等根の三種類となります。
3個の実根が得られた場合は、正の値で、一番小さい値を値を採用します。
a0にゼロが与えられた場合は、二次方程式、a0、a1にゼロが与えられた場合は、一次方程式の根を求めます。
二次方程式の場合、二つの根が得られます。

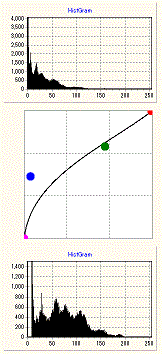
上図は、方程式の根を求めてXからYの値を計算し、補正曲線としたものです。
左側三この図は、前の二つの方法で求めた曲線とは少し違いますが、使用されないので問題はないでしょう。
どちらの方法が良いとは言えません。
テンプレートとして配列テーブルを作成する一番簡単な方法は 2 ⊿tの値を小さくとり、X、Yの値を計算し配列に書き込む方法 が一番簡単です。