アフィン変換
アフィン変換は画像の拡大縮小、平行移動、回転を３×３のマトリックスを使用して、まとめて行うことをですが、詳しい説明は、アフィン変換で他のホームページを検索して下さい。
二次元平面状の単純な変換なので、ここのプログラムでは、通常の計算により、変換を行っています。
ここでも、画像の回転と同じ様に、変換後の座標から、元画像の座標を計算し、座標の値が整数とならない場合は、線形補間法により、変換後の座標の値を求めています。
画像の回転とは、線形補間の計算手順が少し違いますが、同じ計算です。
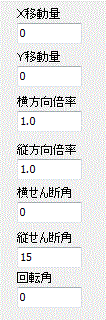入力項目は、左図の項目です。
ここのプログラム例では、Ｘ、Ｙの移動は変倍、せん断、回転等の変形が行われた後、最後に行われます。
実際には、変換後の座標から、元画像の座標を求めて新しい値とする為、計算は最初に行います、計算は変換したい手順と逆の手順で行わないと、正しい変換とはなりません。
移動をいつ行うかですが、回転前に移動して、移動した画像を回転するのか、回転をした後移動を行うかは、使用する目的によって違うかと思います。
又、好みもあり、どの手順が正しいかは、一概に言えないようです。
次のプログラム例は、計算部分だけだけを抜き出してあります。
//**** affine *** 拡大縮小,回転,移動,せん断（線形補間法）*************** // *lueMat: 入力画像配列 // *OutMat: 出力画像配列 // deg: 回転角（度） // r 回転角（rad） // zx: 拡大率（横） // zy: 拡大率（縦） // px: 移動量（横） // py: 移動量（縦） // vtg 縦せん断(度) // vtr 縦せん断(rad) // htg 横せん断(度) // htr 横せん断(rad) //*************************************************************** procedure TForm1.affine(deg, zx, zy, px, py, vtg, htg: Double); var i, j, m, n : Integer; x, y, u, v, p, q : Double; r, c, s : Double; xs, ys, xsp, ysp : Integer; db, dg, dr : Integer; vtr, htr : double; begin r := DegToRad(deg); // 回転角 vtr := tan(DegToRad(vtg)); // 縦せん断角 htr := tan(DegToRad(htg)); // 横せん断角 c := cos(r); s := sin(r); ys := MatSize div 2; // 縦方向中心位置計算 MatSizeは出力用配列の大きさです xs := MatSize div 2; // 横方向中心位置計算 ysp := ys - 1; // ys最大値 (m + ys) < GHeight xsp := xs - 1; // xs最大値 (n + xs) < GWidth if MatSize mod 2 <> 0 then begin // サイズが奇数の場合は１大きく ysp := ys; xsp := xs; end; for i := -ys to ysp - 1 do // 出力ビットマップ縦範囲 for j := -xs to xsp - 1 do begin // 出力ビットマップ横範囲 v := i + py; // 縦シフト u := j - px; // 横シフト y := (u * s + v * c) / zy; // 縦変倍 x := (u * c - v * s) / zx; // 横変倍 y := y + x * vtr; // 縦せん断 x := x - y * htr; // 横せん断 m := floor(y); // 負方向へまるめ 負方向へまるめないと正しい補間値になりません n := floor(x); // 負方向へまるめ q := y - m; // Ｙ方向補正値 小数点以下の値を求めます p := x - n; // Ｘ方向補正値 m := m + ys; // 元図座標Y n := n + xs; // 元図座標X // 線形補間計算 if (m >= 0) and (m < ysp + ys) and (n >= 0) and (n < xsp + xs) then begin db := trunc(((1 - q) * ((1 - p) * BlueMat[m , n ] + P * BlueMat[m , n + 1]) + q * ((1 - p) * BlueMat[m + 1, n ] + P * BlueMat[m + 1, n + 1]))); dg := trunc(((1 - q) * ((1 - p) * GlueMat[m , n ] + P * GlueMat[m , n + 1]) + q * ((1 - p) * GlueMat[m + 1, n ] + P * GlueMat[m + 1, n + 1]))); dr := trunc(((1 - q) * ((1 - p) * RlueMat[m , n ] + P * RlueMat[m , n + 1]) + q * ((1 - p) * RlueMat[m + 1, n ] + P * RlueMat[m + 1, n + 1]))); end else begin // 元画像範囲外は黒 db := 0; dg := 0; dr := 0; end; BOutMat[i + ys,J + xs] := db; // 出力用配列に保存 GOutMat[i + ys,J + xs] := dg; ROutMat[i + ys,J + xs] := dr; end; end;
アフィン変換には透視の変換はありません。
透視にするのは、三次元の変換が必要で、４×４のマトリックスを使用します。
又、透視ではなく、台形にするのは射影変換(ホモグラフィ)と言われていて、変換式も違いますが実行結果は殆ど同じになります。
affine.zip