フーリエ変換（離散）
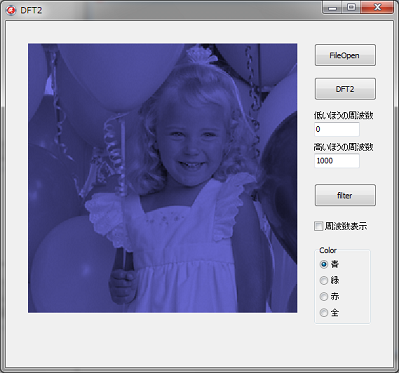画像のフーリエ変換(離散)の説明は、
イメージングソリューションを参照して下さい。
フーリエ変換について、理論的な事が色々説明されていますが、全ての振動波形が、周波数の違う正弦波の重ねあわせで表現できると言うところから成り立っています。
変換は、各周波数の正弦波の波形と、サンプルの波形の相関値の計算を統計的に求めているだけなのですが、色々難しい説明をしてくれています。
統計的処理であるため、変換したものを逆変換しても、完全にもとの波形に戻ることはありませんが、デジタル画像の場合、離散データーのデジタル値なので、元の値を再現する事が出来ます。
画像の周波数分析の利用方法はあまり無いように思われますが、他のサイトで公開されているプログラムを参考にして、Ｄｅｌｐｈｉでプログラムを作成してみました。
フーリエ変換をする場合、非常に計算量が多く、現在の写真画像の場合、いつになったら処理が終了するのか分からないぐらい時間がかかります。
此処で利用している、２５６×２５６位の画像であれば、即計算が終了するので、ストレスを感じることは無いでしょう。
高速で計算できるＦＦＴは、 データーの数が、２の累乗に限られています。
画像サイズが、２の累乗になっていない場合は、ＤＦＴ(discrete fourier transform)を使用しますが、ＦＦＴ(Fast
Fourier Transform)に対して１００倍以上時間が掛かると思われます。
次の画像は、二次元のフーリエ変換を行った場合のサンプル画像です。
単に周波数変換をすると、直流及び低周波成分が四隅に表示されます。
直流及び低周波成分が中央に表示されるように、幅と、高さ方向を二分の一対角方向へ移動すると、下図の低周波中央表示のようになります。
なんとなく、円形に分布しているのが分かります。
右側のサンプル画像は、フィルターを設定しています。
高いほうの周波数をカットすると、ボケたような画像になりますが、ガウシアンフィルターのような綺麗なボケ画像にはなりません。
周波数成分が現れたような、縞模様の入った画像となります。
低いほうをカットすると、直量成分、及び低周波が、画像の明るさに寄与しているので、濃度差の大きい部分を残し暗い画像になります。
フーリエ変換は、色々な周波数の重ねあわせで、元の波形を再現します、その為、フィルターで特定の周波数をカットすると、元の波形の再現は不可能となります。
左の画像は、フィルターを設定し場合の、周波数表示です。
次に周波数変換ルーチンを示します。
プログラム全体は、ダウンロードして下さい。
DFTルーチン
// このルーチンは順変換（画像→フーリエ）、逆変換（フーリエ→画像）両方に使えます // realには実数（順変換では元画像の値）、imageには虚数（はじめは0）が入っています // invは順変換ではfalse、逆変換ではtrue // 変換後の値はreal、imageを書き換えて保存します // 計算がFFTに比べて遅いので、順変換、逆変換で計算を分けています。 procedure TForm1.DFT(var real, image: D2array; inv: boolean); var M2 : Double; Wnorm, Hnorm : Double; RW, RH : Double; Tre, Tim : D2array; WcTable, WsTable : D2array; HcTable, HsTable : D2array; i, j, y, x, xx, yy: Integer; begin // スペクトル変換時はシグマ値をデーター個数で除算して値としますが // スペクトルを画像として表示する時、黒の成分を調整するため // データー数の平方根で除算して、値とし、画像に変換する場合は // 再度データー数の平方根で除算してデーター個数で除算した事にします。 if inv then begin M2 := 2 * PI; Wnorm := 1 / sqrt(X_SIZE); Hnorm := 1 / sqrt(Y_SIZE); // Wnorm := 1.0; // Hnorm := 1.0; end else begin M2 := - 2 * PI; Wnorm := 1 / sqrt(X_SIZE); Hnorm := 1 / sqrt(Y_SIZE); // Wnorm := 1.0 / X_SIZE; // Hnorm := 1.0 / Y_SIZE; end; // 作業用配列確保 SetLength(Tre, X_SIZE, Y_SIZE); SetLength(Tim, X_SIZE, Y_SIZE); SetLength(WcTable, X_SIZE, X_SIZE); SetLength(WsTable, X_SIZE, X_SIZE); SetLength(HcTable, Y_SIZE, Y_SIZE); SetLength(HsTable, Y_SIZE, Y_SIZE); // 変換テーブル生成 直流、低い周波数から 高いほうへ設定 RW := M2 / X_SIZE; RH := M2 / Y_SIZE; for i := 0 to X_SIZE - 1 do for j := 0 to X_SIZE - 1 do begin Wctable[i][j] := cos(i * j * RW); Wstable[i][j] := sin(i * j * RW); end; for i := 0 to Y_SIZE - 1 do for j := 0 to Y_SIZE - 1 do begin Hctable[i][j] := cos(i * j * RH); Hstable[i][j] := sin(i * j * RH); end; // X軸方向DFT // y軸毎に変換 for y := 0 to Y_SIZE - 1 do // 一次元DFT for x := 0 to X_SIZE - 1 do begin Tre[x][y] := 0.0; Tim[x][y] := 0.0; if inv then begin for xx := 0 to X_SIZE - 1 do begin Tre[x][y] := Tre[x][y] + real[xx][y] * Wctable[x][xx] - image[xx][y] * Wstable[x][xx]; Tim[x][y] := Tim[x][y] + real[xx][y] * Wstable[x][xx] + image[xx][y] * Wctable[x][xx]; end; end else for xx := 0 to X_SIZE - 1 do begin Tre[x][y] := Tre[x][y] + real[xx][y] * Wctable[x][xx]; Tim[x][y] := Tim[x][y] + real[xx][y] * Wstable[x][xx]; end; Tre[x][y] := Tre[x][y] * wnorm; Tim[x][y] := Tim[x][y] * wnorm; end; // Y軸方向DFT // X軸毎に変換 for x := 0 to X_SIZE - 1 do // 一次元DFT for y := 0 to Y_SIZE - 1 do begin real[x][y] := 0.0; if inv then begin for yy := 0 to Y_SIZE - 1 do real[x][y] := real[x][y] + Tre[x][yy] * Hctable[y][yy] - Tim[x][yy] * Hstable[y][yy]; end else begin image[x][y] := 0.0; for yy := 0 to Y_SIZE - 1 do begin real[x][y] := real[x][y] + Tre[x][yy] * Hctable[y][yy] - Tim[x][yy] * Hstable[y][yy]; image[x][y] := image[x][y] + Tre[x][yy] * Hstable[y][yy] + Tim[x][yy] * Hctable[y][yy]; end; image[x][y] := image[x][y] * Hnorm; end; real[x][y] := real[x][y] * Hnorm; end; end;
ＦＦＴルーチン
//--- rvmtx2 --- ２次元データの転置 ------------------------------------------- // a: ２次元入力データ // b: ２次元出力データ // xsize: 水平データ個数 // ysize: 垂直データ個数 //----------------------------------------------------------------------------- procedure TForm1.rvmtx2(var a, b: D2array; xsize, ysize: integer); var i, j: integer; begin for i := 0 to ysize - 1 do for j := 0 to xsize - 1 do b[i, j] := a[j, i]; end; //--- rvmtx1 --- ２次元データの転置 ------------------------------------------- // a: ２次元入力データ // b: ２次元出力データ // xsize: 水平データ個数 // ysize: 垂直データ個数 //----------------------------------------------------------------------------- procedure TForm1.rvmtx1(var a, b: D2array; xsize, ysize: Integer); var i, j: integer; begin for i := 0 to ysize - 1 do for j := 0 to xsize - 1 do b[j, i] := a[i, j]; end; //--- birv --- データの並べ換え ----------------------------------------------- // a: データの配列 // length: データ個数 // ex: データ個数を２の累乗で与えます(2のex乗個） // b: 作業用バッファ //----------------------------------------------------------------------------- procedure TForm1.birv(a: PDarray; length, ex: Integer; b: PDarray); var i, ii, k, bit : Integer; begin for i := 0 to length - 1 do begin ii := i; bit:= 0; for k := 0 to ex do begin bit := (ii and 1) or bit; if k = ex - 1 then break; bit := bit shl 1; ii := ii shr 1; end; b[i] := a[bit]; end; for i := 0 to length - 1 do a[i] := b[i]; end; //--- fft1core --- １次元ＦＦＴの計算の核になる部分 --------------------------- // a_rl: データ実数部（入出力兼用） // a_im: データ虚数部（入出力兼用） // ex: データ個数を２の累乗で与えます(2のex乗個） // sin_tbl: SIN計算用テーブル // cos_tbl: COS計算用テーブル //----------------------------------------------------------------------------- procedure TForm1.fft1core(a_rl, a_im: PDarray; length, ex: integer; sin_tbl, cos_tbl, buf: PDarray); var i, j, k, w, j1, j2 : Integer; numb, lenb, timb : Integer; xr, xi, yr, yi, nrml : Double; begin if OPT = 1 then begin // OPT = 1 光学的ＤＦＴ（直流分が中央） j := 1; Repeat // for j = 1 to length - 1 step 2 do と同じ a_rl[j] := - a_rl[j]; a_im[j] := - a_im[j]; j := j + 2; until j > length - 1; end; numb := 1; lenb := length; for i := 0 to ex - 1 do begin lenb := lenb div 2; timb := 0; for j := 0 to numb - 1 do begin w := 0; for k := 0 to lenb - 1 do begin j1 := timb + k; j2 := j1 + lenb; xr := a_rl[j1]; xi := a_im[j1]; yr := a_rl[j2]; yi := a_im[j2]; a_rl[j1] := xr + yr; a_im[j1] := xi + yi; xr := xr - yr; xi := xi - yi; a_rl[j2] := xr * cos_tbl[w] - xi * sin_tbl[w]; a_im[j2] := xr * sin_tbl[w] + xi * cos_tbl[w]; w := w + numb; end; timb := timb + 2 * lenb; end; numb := numb * 2; end; birv(a_rl, length, ex, buf); // 実数データの並べ換え birv(a_im, length, ex, buf); // 虚数データの並べ換え if OPT = 1 then begin // OPT = 1 光学的ＤＦＴ（直流分が中央） j := 1; Repeat // for j = 1 to length - 1 step 2 do と同じ a_rl[j] := - a_rl[j]; a_im[j] := - a_im[j]; j := j + 2; until j > length - 1; end; nrml := 1.0 / sqrt(length); // 本来は Σ値をデーター数で除算しますがスペクトル表示の為平方根で除算 for i := 0 to length - 1 do begin // 画像に再変換する場合は、２回除算されるのでデーター数で除算された事になります a_rl[i] := a_rl[i] * nrml; a_im[i] := a_im[i] * nrml; end; end; //--- cstb --- SIN,COSテーブル作成 -------------------------------------------- // length: データ個数 // inv: 1: ＤＦＴ, -1: 逆ＤＦＴ // sin_tbl: SIN計算用テーブル // cos_tbl: COS計算用テーブル //----------------------------------------------------------------------------- procedure TForm1.cstb(length: Integer; inv: Integer; var sin_tbl, cos_tbl: array of double); var i : Integer; xx, arg : Double; begin xx := - PI * 2.0 / length; if inv < 0 then xx := - xx; for i := 0 to length - 1 do begin arg := i * xx; sin_tbl[i] := sin(arg); cos_tbl[i] := cos(arg); end; end; //--- fft2 --- ２次元ＦＦＴの実行 --------------------------------------------- // （GWidth，GHeightが２のべき乗の場合に限ります） // a_rl: データ実数部（入出力兼用） // a_im: データ虚数部（入出力兼用） // inv: 1: ＤＦＴ，-1: 逆ＤＦＴ // X_EXP: ex: データ個数を２の累乗で与えます(2のex乗個） // Y_EXP: ey: データ個数を２の累乗で与えます(2のey乗個） //----------------------------------------------------------------------------- function TForm1.FFT2(var a_rl, a_im: D2array; inv, Y_EXP, X_EXP: Integer): Integer; var b_rl : D2array; // データ転置作業用配列（実数部） b_im : D2array; // データ転置作業用配列（虚数部) hsin_tbl : array of Double; // 水平用SIN計算用テーブル hcos_tbl : array of Double; // 水平用COS計算用テーブル vsin_tbl : array of Double; // 垂直用SIN計算用テーブル vcos_tbl : array of Double; // 垂直用COS計算用テーブル buf_x : array of Double; // 作業用バッファ（水平方向） buf_y : array of Double; // 作業用バッファ（垂直方向） i : Integer; begin // 配列の確保 SetLength(b_rl, GWidth, GHeight); SetLength(b_im, GWidth, GHeight); SetLength(hsin_tbl, GWidth); SetLength(hcos_tbl, GWidth); SetLength(vsin_tbl, GHeight); SetLength(vcos_tbl, GHeight); SetLength(buf_x, GWidth); SetLength(buf_y, GHeight); if (b_rl = nil) or (b_im = nil) or (hsin_tbl = nil) or (hcos_tbl = nil) or (vsin_tbl = nil) or (vcos_tbl = nil) or (buf_x = nil) or (buf_y = nil) then begin Result := -1; exit; end; cstb(GWidth, inv, hsin_tbl, hcos_tbl); // 水平用SIN,COSテーブル作成 cstb(GHeight, inv, vsin_tbl, vcos_tbl); // 垂直用SIN,COSテーブル作成 // 水平方向のＦＦＴ for i := 0 to GHeight - 1 do fft1core(@a_rl[i][0], @a_im[i][0], GWidth, X_EXP, @hsin_tbl[0], @hcos_tbl[0], @buf_x[0]); // ２次元データの転置 rvmtx1(a_rl, b_rl, GWidth, Gheight); rvmtx1(a_im, b_im, GWidth, Gheight); // 垂直方向のＦＦＴ for i := 0 to GWidth - 1 do fft1core(@b_rl[i][0], @b_im[i][0], GHeight, Y_EXP, @vsin_tbl[0], @vcos_tbl[0], @buf_y[0]); //* ２次元データの転置 rvmtx2(b_rl, a_rl, GWidth, GHeight); rvmtx2(b_im, a_im, GWidth, GHeight); result := 0; end;
サンプル画像は、カラーになっていますが、タウンロードプログラムの中には、グレー（輝度変換)のプログラムもあります。
カラーの場合、三色に分解して、色毎にフーリエ変換を行うので、時間が三倍掛かります。
輝度と、色信号にして周波数解析も行ってみましたが、計算量が増えるので、時間が増えるだけであることがわかりました。
FFT.zip